Department of Phonetics and Linguistics
THE SINGLE-LAYER PERCEPTRON AS A MODEL OF HUMAN CATEGORISATION BEHAVIOUR(Section 5)
Roel SMITS & Louis TEN BOSCH
(continued from...)
6. Summary and conclusions
Although perceptrons have become popular categorisation models,
a formal description of the properties of such a model in the
human categorisation context seems to be lacking. This paper puts
forward a descriptive model of human categorisation behaviour
in which the single-layer perceptron (SLP) is the central part.
The model is discussed within Ashby's representation-retrieval-response
selection framework and its modelling properties are studied.
It appears to be useful to separate an average component and a
differential component in the ratio of the response probabilities
for two competing classes. The differential component exclusively
determines the location of the equal-probability boundary between
the two classes. The equal-probability boundaries of the model
are shown to be linear functions of the feature vector. The average
component effectively "scales" the contribution of the
differential component. In one extreme case of scaling the SLP-based
model is shown to be equivalent to an asymptotic instance of the
well-known similarity-choice model. It is also shown that, due
to the scaling, the model's probability functions may have local
extrema in the feature space.
Connectionist models, such as our SLP-based model, generally have
a large number of parameters to be estimated, which may lead to
overfitting. This is one of the reasons why the use of connectionist
models in psychological research continues to meet with suspicion.
We propose a way in which a cross-validation technique called
the "leaving-one-out" method can be used in the context
of human classification data. After our model has been fitted
on a data set, the technique gives an estimate of the model's
generalisability, that is, the model's goodness-of-fit on data
which have not been used in the model estimation procedure. The
proposed technique is not specific to the SLP-based model and
can be used for any classification model.
Go to Appendices
Acknowledgements
The research reported in this paper was carried out at the Institute
for Perception Research (IPO) in Eindhoven, The Netherlands. The
authors thank Rudi van Hoe, Don Bouwhuis, B. Yegnanarayana and
Yves Kamp for their helpful and constructive criticism, and Rene
Collier for his patience. Louis ten Bosch is with Lernout and
Hauspie Speech Products, Wemmel, Belgium.
References
Ashby, F.G. (1992) Multidimensional models of categorization.
In: F.G. Ashby (Ed.), Multidimensional models of perception
and cognition. Hillsdale, New Jersey: Lawrence Erlbaum.
Ashby, F.G., & Perrin, N.A. (1988) Toward a unified theory
of similarity and recognition. Psychological Review 95,
124-150.
Blumstein, S.E., and Stevens, K.N. (1979) Acoustic invariance
in speech production: Evidence from measurements of the spectral
characteristics of stop consonants. Journal of the Acoustical
Society of America 66, 1001-1017.
Blumstein, S.E., and Stevens, K.N. (1980) Perceptual invariance
and onset spectra for stop consonants in different vowel environments.
Journal of the Acoustical Society of America 67, 648-662.
Fukunaga, K. (1972) Introduction to statistical pattern recognition.
New York: Academic Press.
Fukunaga, K., & Kessell, D.L. (1971) Estimation of classification
error. IEEE Transactions on Computers 20, 1521-1527.
Gluck, M.A., and Bower, G.H. (1988) From conditioning to category
learning: An adaptive network model. Journal of Experimental
Psychology: General 117, 227-247.
Halle, M., Hughes, G.W., and Radley, J.-P.A. (1957) Acoustic properties
of stop consonants. Journal of the Acoustical Society of America
29, 107-116.
Haykin, S. (1994) Neural networks - A comprehensive Foundation.
New York: Macmillan College Publishing Company.
Hertz, J., Krogh, A., & Palmer, R.G. (1991) Introduction
to the theory of neural computation. Redwood City: Addison-Wesley.
Kewley-Port, D., Pisoni, D.B., & Studdert-Kennedy, M. (1983)
Perception of static and dynamic acoustic cues to place of articulation
in initial stop consonants. Journal of the Acoustical Society
of America 73, 1779-1793.
Kruschke, J.K. (1992) ALCOVE: An examplar-based connectionist
model of category learning. Psychological Review 99, 22-44.
Kruskal, J.B. (1964) Multidimensional scaling by optimizing goodness
of fit to a nonmetric hypothesis. Psychometrika 29, 1-27.
Lippman, R.P. (1987) An introduction to computing with neural
nets. IEEE ASSP Magazine 4, 4-22.
Luce, R.D. (1963) Detection and recognition. In: R.D. Luce, R.R.
Bush, and S.E. Galanter (Eds.), Handbook of mathematical psychology,
vol. 1, ch. 3, New York: Wiley.
Massaro, D.W. (1988) Some criticisms of connectionist models of
human performance. Journal of Memory and Language 27, 213-234.
McClelland, J.L., Rumelhart, D.E., and the PDP research group
(1986) Parallel distributed processing: Explorations in the
microstructure of cognition. Cambridge, MA: MIT press.
Nosofsky, R.M. (1986) Attention, similarity, and the identification-categorization
relationship. Journal of Experimental Psychology: General 115,
39-57.
Nosofsky, R.M., and Smith, J.E.K. (1992) Similarity, identification,
and categorization: Comment on Ashby and Lee (1991). Journal
of Experimental Psychology: General 121, 237-245.
Oden, G.C., and Massaro, D.W. (1978) Integration of featural information
in speech perception. Psychological Review 85, 172-191.
Quinlan, P. (1991) Connectionism and Psychology. Hemel
Hempstead: Harvester Wheatsheaf.
Shepard, R.N. (1958) Stimulus and response generalization: tests
of a model relating generalization to distance in psychological
space. Journal of Experimental Psychology 55, 509-523.
Smits, R. (1995) Detailed versus global spectro-temporal cues
for the perception of stop consonants. Doctoral dissertation,
Institute for Perception Research (IPO), Eindhoven, Netherlands.
Smits, R., Ten Bosch, L., & Collier, R. (1995a) Evaluation
of various sets of acoustical cues for the perception of prevocalic
stop consonants: I. Perception experiment. Accepted for Journal
of the Acoustical Society of America.
Smits, R., Ten Bosch, L., & Collier, R. (1995b) Evaluation
of various sets of acoustical cues for the perception of prevocalic
stop consonants: II. Modeling and evaluation. Accepted for Journal
of the Acoustical Society of America.
Ten Bosch, L., & Smits, R. (1996) On error criteria in perception
modeling. In preparation.
Appendix 1
In this appendix it is shown that the SLP and the SCM coincide
in the limit case, when the SLP-biases tend to 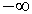 and the distance of all prototypes to the origin approach infinity.
We assume that all stimulus features are normalised using Eq.
(7), so that all values are grouped around the origin.
and the distance of all prototypes to the origin approach infinity.
We assume that all stimulus features are normalised using Eq.
(7), so that all values are grouped around the origin.
Let us first define the SCM processing stages. Each response class
Cj has one prototype 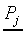 which is a vector containing NF components Pjk.
The weighted Euclidean distance dij of a stimulus
Si to prototype
which is a vector containing NF components Pjk.
The weighted Euclidean distance dij of a stimulus
Si to prototype 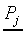 is defined as
is defined as
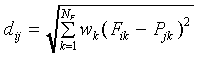
|
(A1)
|
where wk is a non-negative parameter representing
the attention allocated to feature dimension k.
It is assumed that the similarity sij of stimulus
Si to category Cj is related
to the psychological distance dij of stimulus
Si to prototype 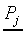 via the exponential
decay function (e.g. Shepard, 1958):
via the exponential
decay function (e.g. Shepard, 1958):
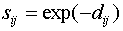
|
(A2)
|
Finally, the probability pij of responding class
Cj, given stimulus Si is defined
as (Luce, 1963):
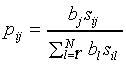
|
(A3)
|
where 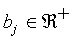 is the response bias for category
Cj. Note that this response bias is different
from the SLP-bias.
is the response bias for category
Cj. Note that this response bias is different
from the SLP-bias.
Now, first it is to be shown that the distance between F
and 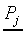 is linear in F when
is linear in F when  tends to
tends to 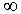 . Let
. Let 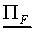 represent the orthogonal projection of the feature vector F
on the prototype vector
represent the orthogonal projection of the feature vector F
on the prototype vector 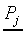 of class Cj,
in the vector space with dotproduct
of class Cj,
in the vector space with dotproduct
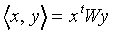
|
(A4)
|
W denoting the diagonal matrix of attention weights.
Since 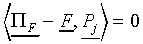 by definition, it follows that
the distance dj of F to prototype
by definition, it follows that
the distance dj of F to prototype
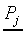 equals
equals
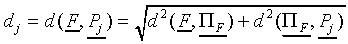
|
(A5)
|
Since
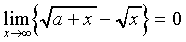
|
(A6)
|
it follows that
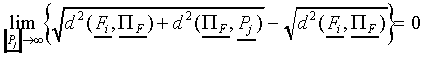
|
(A7)
|
Thus, when  is large, we find
is large, we find
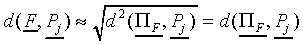
|
(A8)
|
Because 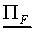 and
and 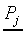 have the same direction
have the same direction
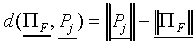
|
(A9)
|
After some calculation, it follows that
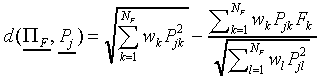
|
(A10)
|
Hence, 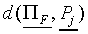 is a linear function of F.
is a linear function of F.
If we substitute
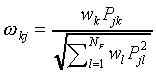
|
(A11)
|
Eq. (A10) simplifies to
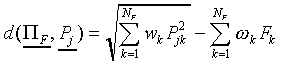
According to Shepard (1958) and Luce (1963), the biased similarity
bjsj of F to 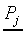 is defined by
is defined by
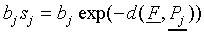
|
(A12)
|
If  is large
is large
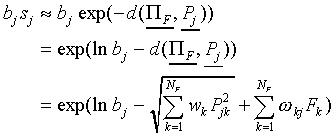
|
(A13)
|
If we now substitute
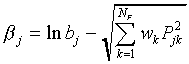
|
(A14)
|
Eq. (A13) simplifies to
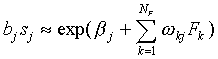
|
(A15)
|
Let us now turn to the SLP. As stated in Eq. (5), the function
sj is defined as
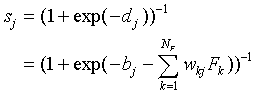
|
(A16)
|
Using
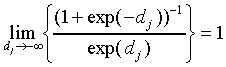
|
(A17)
|
we find that
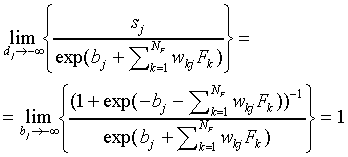
|
(A18)
|
Thus, we find for bj < 0 and 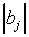 large
large
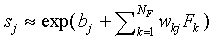
|
(A19)
|
Expression (A19) is equivalent to Eq. (A15) for the similarity
of the SCM with the prototypes 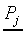 at infinite distance
from the origin. Thus we find that, in this limit case, the SLP-biases
bj are equivalent to the SCM parameters
at infinite distance
from the origin. Thus we find that, in this limit case, the SLP-biases
bj are equivalent to the SCM parameters 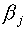 ,
which stand for
,
which stand for 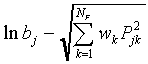 , and the SLP-weights
wkj
, and the SLP-weights
wkj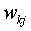 are equivalent to the SCM
parameters
are equivalent to the SCM
parameters 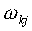 , which stand for
, which stand for 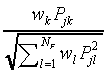 (see Table 1).
(see Table 1).
Appendix 2
In this appendix it is shown that locally extremal points can
exist in the SLP-based model with arbitrary number of classes
and dimension of feature space. Only the case of p1(F)
is considered. Other classes follow by symmetry.
The SLP with NF input nodes and Nr
output nodes defines Nr linear functions
di(F), i = 1,…, Nr.
In full, 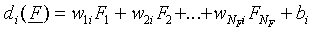 . After choice rule, we get
. After choice rule, we get
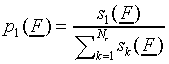
|
(A20)
|
Implicitly, si depends on the coefficients wji,
the bias bi, and the vector F.
Differentiating, we obtain
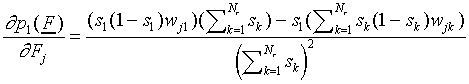
|
(A21)
|
which should vanish for each j. Using the fact that s1
> 0, 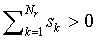 , this leads to
, this leads to
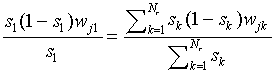
|
(A22)
|
for all j. It is our purpose to prove that the w11,
w21,…, b1 can be found
such that Eq. (A22) holds for each j, given the other coefficients
wji and bi for which i
> 1. So we assume the values of si, i
> 1, to be specified beforehand. Also the wji
and the bi i > 1 are given, as is
F. Let us denote
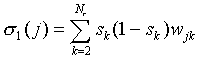
|
(A23)
|
and
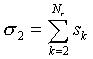
|
(A24)
|
We obtain
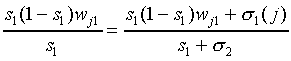
|
(A25)
|
which implies
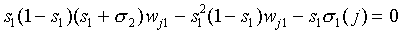
|
(A26)
|
which yields (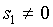 )
)
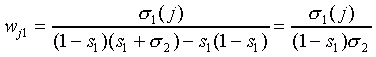
|
(A27)
|
So all we have to do is to choose the wj1
and b1 in such a way that Eq. (A27) holds, in
which 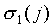 and
and 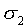 depend
on F and on the chosen predefined coefficients wjk
and bk, k > 1. We have the small problem
that s1 in the right-hand side itself depends
on the wj1. To solve this, we can
first choose the wj1 to be equal
to
depend
on F and on the chosen predefined coefficients wjk
and bk, k > 1. We have the small problem
that s1 in the right-hand side itself depends
on the wj1. To solve this, we can
first choose the wj1 to be equal
to 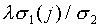 where
where 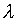 can
be chosen larger than 1 independent of j. Secondly, we
can manipulate the last remaining degree of freedom b1
to match
can
be chosen larger than 1 independent of j. Secondly, we
can manipulate the last remaining degree of freedom b1
to match 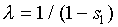 (this means
(this means 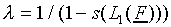 .
This uniquely specifies b1. Observe that the
direction of the normal of d1 is always uniquely
determined by the other di and F,
and that b1 is nonlinearly determined by the
actual choice of the length of the normal, i.e., by the wj1.
.
This uniquely specifies b1. Observe that the
direction of the normal of d1 is always uniquely
determined by the other di and F,
and that b1 is nonlinearly determined by the
actual choice of the length of the normal, i.e., by the wj1.
This shows that it is possible, in general, for p1(F)
to have a local extremum for bounded F, if we can
manipulate the position of the d1 while the
di, i > 1 are prespecified. The same
reasoning holds, mutatis mutandis, for the other classes.
In the limit case of 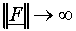 , s1
will in general tend to 0 or 1 (only in particular cases this
will not be the case). In any case
, s1
will in general tend to 0 or 1 (only in particular cases this
will not be the case). In any case 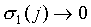 for
each
for
each 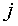 , since
, since 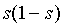 will in general tend to 0. So, if
will in general tend to 0. So, if 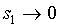 ,
, 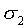 must tend to 0 to avoid degeneration, which means that every sk,
k > 1, must tend to 0. On the other hand, if
must tend to 0 to avoid degeneration, which means that every sk,
k > 1, must tend to 0. On the other hand, if 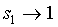 ,
,
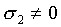 to avoid degeneration, which implies
that at least one of the other sk, k
> 1, must tend to 1. Both these cases reveal something of the
structure of the hyperplanes in case of the SLP. Apparently, a
local extremal point can only exist if there is a real competition
between the classes (i.e., a case in which just one of the si
tends to 1 and the others tend to zero will never yield an extremal
value for
to avoid degeneration, which implies
that at least one of the other sk, k
> 1, must tend to 1. Both these cases reveal something of the
structure of the hyperplanes in case of the SLP. Apparently, a
local extremal point can only exist if there is a real competition
between the classes (i.e., a case in which just one of the si
tends to 1 and the others tend to zero will never yield an extremal
value for 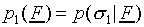 for bounded F).
And if there is such a competition, a local extremum can be forced
to exist in every F by manipulating the corresponding
hyperplane.
for bounded F).
And if there is such a competition, a local extremum can be forced
to exist in every F by manipulating the corresponding
hyperplane.
© 1996 Roel Smits and Louis Ten Bosch
 Back to SHL 9 Contents
Back to SHL 9 Contents
 Back to Publications
Back to Publications
 Back to Phonetics and Linguistics Home Page
Back to Phonetics and Linguistics Home Page
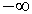 and the distance of all prototypes to the origin approach infinity.
We assume that all stimulus features are normalised using Eq.
(7), so that all values are grouped around the origin.
and the distance of all prototypes to the origin approach infinity.
We assume that all stimulus features are normalised using Eq.
(7), so that all values are grouped around the origin.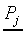 which is a vector containing NF components Pjk.
The weighted Euclidean distance dij of a stimulus
Si to prototype
which is a vector containing NF components Pjk.
The weighted Euclidean distance dij of a stimulus
Si to prototype 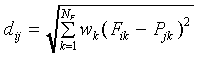
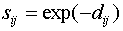
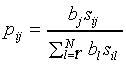
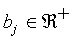 is the response bias for category
Cj. Note that this response bias is different
from the SLP-bias.
is the response bias for category
Cj. Note that this response bias is different
from the SLP-bias. tends to
tends to 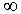 . Let
. Let 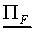 represent the orthogonal projection of the feature vector F
on the prototype vector
represent the orthogonal projection of the feature vector F
on the prototype vector 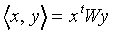
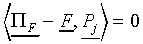 by definition, it follows that
the distance dj of F to prototype
by definition, it follows that
the distance dj of F to prototype
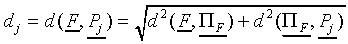
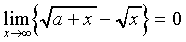
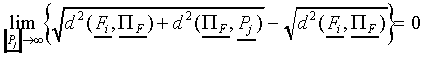
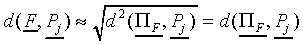
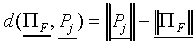
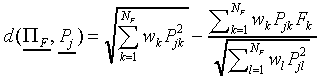
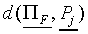 is a linear function of F.
is a linear function of F.
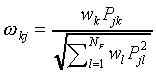
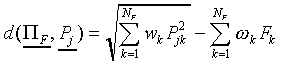
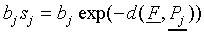
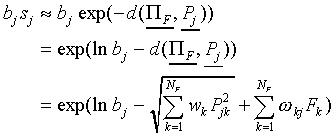
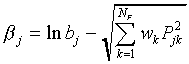
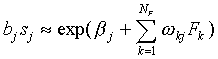
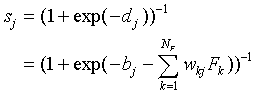
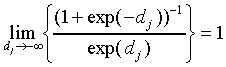
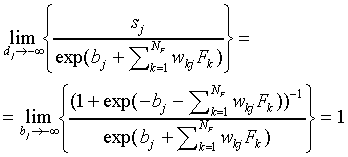
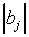 large
large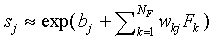
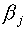 ,
which stand for
,
which stand for 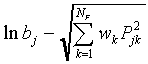 , and the SLP-weights
wkj
, and the SLP-weights
wkj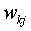 are equivalent to the SCM
parameters
are equivalent to the SCM
parameters 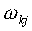 , which stand for
, which stand for 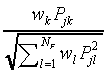 (see Table 1).
(see Table 1).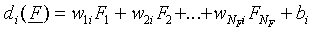 . After choice rule, we get
. After choice rule, we get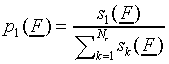
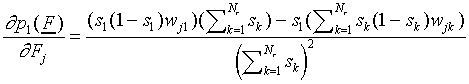
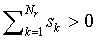 , this leads to
, this leads to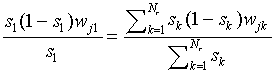
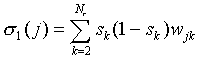
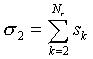
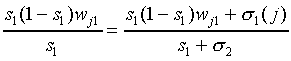
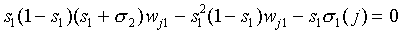
 )
)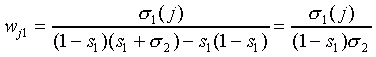
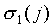 and
and 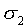 depend
on F and on the chosen predefined coefficients wjk
and bk, k > 1. We have the small problem
that s1 in the right-hand side itself depends
on the wj1. To solve this, we can
first choose the wj1 to be equal
to
depend
on F and on the chosen predefined coefficients wjk
and bk, k > 1. We have the small problem
that s1 in the right-hand side itself depends
on the wj1. To solve this, we can
first choose the wj1 to be equal
to 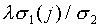 where
where 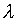 can
be chosen larger than 1 independent of j. Secondly, we
can manipulate the last remaining degree of freedom b1
to match
can
be chosen larger than 1 independent of j. Secondly, we
can manipulate the last remaining degree of freedom b1
to match 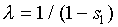 (this means
(this means 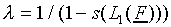 .
This uniquely specifies b1. Observe that the
direction of the normal of d1 is always uniquely
determined by the other di and F,
and that b1 is nonlinearly determined by the
actual choice of the length of the normal, i.e., by the wj1.
.
This uniquely specifies b1. Observe that the
direction of the normal of d1 is always uniquely
determined by the other di and F,
and that b1 is nonlinearly determined by the
actual choice of the length of the normal, i.e., by the wj1.
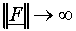 , s1
will in general tend to 0 or 1 (only in particular cases this
will not be the case). In any case
, s1
will in general tend to 0 or 1 (only in particular cases this
will not be the case). In any case 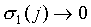 for
each
for
each 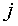 , since
, since 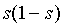 will in general tend to 0. So, if
will in general tend to 0. So, if 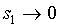 ,
, 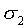 must tend to 0 to avoid degeneration, which means that every sk,
k > 1, must tend to 0. On the other hand, if
must tend to 0 to avoid degeneration, which means that every sk,
k > 1, must tend to 0. On the other hand, if 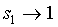 ,
,
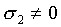 to avoid degeneration, which implies
that at least one of the other sk, k
> 1, must tend to 1. Both these cases reveal something of the
structure of the hyperplanes in case of the SLP. Apparently, a
local extremal point can only exist if there is a real competition
between the classes (i.e., a case in which just one of the si
tends to 1 and the others tend to zero will never yield an extremal
value for
to avoid degeneration, which implies
that at least one of the other sk, k
> 1, must tend to 1. Both these cases reveal something of the
structure of the hyperplanes in case of the SLP. Apparently, a
local extremal point can only exist if there is a real competition
between the classes (i.e., a case in which just one of the si
tends to 1 and the others tend to zero will never yield an extremal
value for 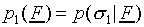 for bounded F).
And if there is such a competition, a local extremum can be forced
to exist in every F by manipulating the corresponding
hyperplane.
for bounded F).
And if there is such a competition, a local extremum can be forced
to exist in every F by manipulating the corresponding
hyperplane. Back to SHL 9 Contents
Back to SHL 9 Contents

