Department of Phonetics and Linguistics
1. Introduction
Categorisation plays an important role in everyday processes of
perception and cognition, such as the recognition of spoken and
written language. A number of formal models for the categorisation
process have been developed , such as the similarity-choice model
(SCM, Shepard, 1958; Luce, 1963), multi-dimensional scaling (MDS,
Kruskal, 1964), the fuzzy logical model of perception (Oden and
Massaro, 1978), multiple-exemplar models (Nosofsky, 1986), and
general recognition theory (GRT, Ashby and Perrin, 1988).
During the last decade, connectionist models have become very
popular, not in the least for the modelling of perceptual and
cognitive processes (e.g. McClelland, Rumelhart and the PDP research
group, 1986; Quinlan, 1991). The multi-layer perceptron (MLP)
is probably the mathematically best-developed connectionist model
(e.g. Lippman, 1987; Hertz, Krogh and Palmer, 1991; Haykin, 1994),
and is currently widely applied as an engineering tool. Within
the field of psychology, a number of formal perceptron-related
models have been developed to describe category learning (e.g.
Gluck and Bower, 1988; Kruschke, 1992). Essential in these models
are the adaptive properties of the connection weights during a
training procedure. Typically, the model performance is evaluated
by studying correct classification rate as a function of training
epochs.
Although the perceptron has also been used as a model of the human
categorisation process itself (rather than the learning
of this process), a formal set-up of the model in this context
as well as a study of its modelling properties and capacities
seems to be lacking. As a result, the perceptron is easily misused
as a model of human categorisation behaviour, and continues to
meet with considerable suspicion, as it is considered to be too
powerful or unconstrained a model which is easily "overfitted"
and which does not allow for the extraction of knowledge from
its parameters (e.g. Massaro, 1988).
It is the purpose of this paper to fill parts of the knowledge
gap mentioned above. In this paper, we will restrict ourselves
to a model based on the single-layer perceptron (SLP)1. The model
we will be presenting is intended purely as a model of human categorisation
behaviour, not of the learning of this behaviour. Furthermore,
we do not claim that the details of the processing within the
SLP-based model embody actual psychological mechanisms. Thus,
the model is simply intended as an analysis tool for categorisation
data. Nevertheless, we will show that fundamental knowledge on
human categorisation mechanisms can be extracted from a fitted
SLP-based model by studying aspects the model's input-output relation.
On issue 1, the estimation of a perceptron on a set of data, a
considerable amount of literature is available (e.g. Hertz, Krogh
and Palmer, 1991; Haykin, 1994). Therefore we will not expand
on in this issue here. Issue 3 is closely related to the model's
properties and capacities which will be treated first. In the
sections 2 and 3 we will set up the general model structure and
discuss the mathematics of the SLP. On the basis of the mathematical
expressions as well as a number of examples we will discuss the
SLP's modelling properties and how to interpret a model which
is fitted on an actual data set. In section 4 we will discuss
issue 2. As indicated earlier, the perceptron, often having a
great many parameters to be estimated, can easily be overfitted.
We therefore present a practical method for estimating the generalizability
of particular estimates of the SLP-based model. Some of the proposed
methods are not specific for the SLP-based model and can also
be used with other categorisation models. Finally, in chapter
5 the comprehensive methodology is illustrated by a practical
example which deals with the issue of the perception of stop consonants.
2. General model structure and definitions
In each trial in a categorisation experiment a subject is presented
with one of Ns stimuli and is required to assign
one of Nr predefined labels to this stimulus.
Essentially, Nr < Ns. For
the sake of simplicity, we will assume that each of the Ns
stimuli is presented to the subject Np times.
Furthermore, we will assume that in each trial the categorisation
of the presented stimulus does not depend on previous trials.
On the basis of this assumption, the results of the experiment
can, without loss of information, be summarised in a stimulus-response
matrix consisting of Ns rows and Nr
columns. Each entry Rij in the stimulus-response
matrix denotes the number of times the stimulus Si
has been labelled as belonging to category Cj.
Note that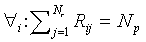 
and 
.
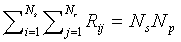We will now propose a model which simulates the mapping of a set
of stimuli onto a set of categorical responses. The proposed model
consists of 3 steps:
These steps can be described as a cascade, as is shown in Figure
1.
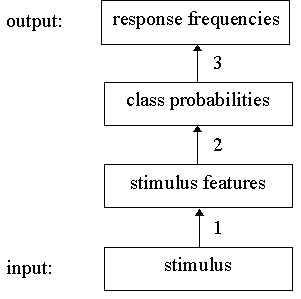
Figure 1. Schematic representation of the model for perceptual
classification. 1, 2, and 3 indicate the representation stage,
retrieval stage, and response selection stage, respectively.
The model fits into the general framework described by Ashby (1992),
which consists of 3 stages: the representation stage, the
retrieval stage and the response selection stage.
In the representation stage the stimulus Si
is transformed from the physical domain into an internal representation,
which is a vector containing NF stimulus features.
Thus, in the representation stage, each stimulus is mapped to
a point in an NF -dimensional feature space
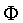. Feature vectors in 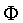will
be denoted by F, the value of F
for stimulus Si is denoted by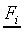 
,
and the kth component of 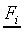, that is, the value
of feature k of stimulus Si, is denoted
by Fik. Generally, the specific choice of features
in a model will be based on either knowledge of the potential
perceptual relevance of various stimulus features or on knowledge
of statistics of the stimulus set. Often, in the preparation
of the experimental stimuli, a number of stimulus features is
explicitly manipulated in order to test their perceptual relevance.
The feature extraction is assumed to be deterministic, which means
that each presentation of a particular stimulus will lead to the
same feature vector, that is, this stage is noise-less.
In the retrieval stage the feature vector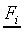
of each stimulus Si is mapped to a vector 
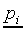of length Nr containing the probabilities of
choosing each of the response categories. The jth component
of the probability vector 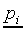is denoted by Pij.
The feature-to-class-probability mapping is assumed to be deterministic.
Here, it is modelled by the SLP.
In the response selection stage the actual labelling takes
place. This labelling is assumed to be probabilistic, and it is
here modelled by a multinomial function. Suppose that after Np
presentations of stimulus Si, a subject has
generated an output vector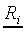 
of length
Nr. Each component Rij of
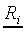denotes the number of times the subject has assigned
stimulus Si to class Cj. The
multinomial model states that the probability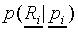 
of generating the response vector 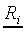after Np
presentations of stimulus Si, given class probabilities
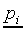, equals
 |
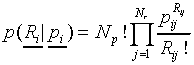(1) |
The 3-stage mapping can be summarised as follows:
 |
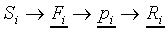(2) |
Back to SHL 9 Contents
Back to Phonetics and Linguistics Home Page
