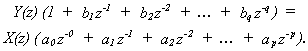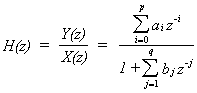UNIT
4:
DIGITAL
SYSTEM MODELS
Summary
This
unit is concerned with the description of digital systems, it introduces the
concepts of a linear time-invariant system, convolution, the general system
difference equation and its implementation, and the frequency response
characteristics of systems.
When you have worked through this unit you should:
· be able to define the
characteristics of a linear, time-invariant system
· understand what is
represented by an impulse response and a frequency response of a system
· be able to explain how
and why systems may be simulated with discrete convolution
· understand how a system
can be described with the general difference equation
· be able to describe one
direct form method for the implementation of the general difference equation in
an algorithm
· be able to state the
z-transform of a sampled sequence
· appreciate that the
z-transform may be used to obtain a polynomial statement of the general
difference equation.
· understand how the response
of a system may be stated in terms of poles and zeros
· understand that the
response can be evaluated for any particular frequency to get the frequency
response graph of a system
· know how to use an
algorithm for implementing an LTI system and calculating its response
· be able to relate the
parameters of a simple resonator to its implementation
Concepts
We
are concerned with systems that transform one digital signal into another, in
particular with systems that perform a linear
processing that does not change with time (is time-invariant). We seek to
describe the behaviour of such systems and to find a general algorithmic
description suitable for digital implementation.
Generally
we describe systems that modify signals in terms of their Frequency Response (a graph of system response against frequency)
and their Phase Response (a graph of
phase shift against frequency). A
linear time-invariant (LTI) system may also be described in the time-domain by
means of its Impulse response, that
is: the graph of the output of the system after an impulse is presented on its
input. This is possible because we can
describe any digital signal as a sequence of impulses of a height equal to the
signal amplitude occurring at the sampling instants. The output of a LTI system to any signal can therefore be
predicted by a suitable linear combination of impulse responses starting at
each sample instant (this is a consequence of the principle of superposition).
Mathematically,
this process can be described as taking a signal x[] and an impulse response
h[] and calculating each output sample y[n] with the formula:
|
|
Assuming
h[] is zero at negative times, and samples are counted from 1. The operation is analogous to laying the
impulse response backwards alongside the input signal prior to n and then cross multiplying and adding.
This process is known as convolution.
y[n] is said to be generated by the convolution of x[] and h[].
Convolution
with the impulse response is the time-domain equivalent of multiplying by the
frequency response. You can see this by
considering convolution of h[] with a sinusoid signal given by:
![]()
so that the output of the system is given by:
![]()
which can be rewritten as:
![]()
That is the output is also a
sinusoid, at the same frequency as the input, but with an amplitude scaling and
a phase change given by H(f).
The
impulse response of a simple resonator is simply an exponentially decaying
sinewave of a frequency equal to the natural frequency and of a rate of decay
related to the bandwidth.
Systems
that have some kind of 'memory' can have impulse responses of infinite duration
(called Infinite-Impulse-Response or IIR
systems), others have an impulse response of finite duration (called
Finite-Impulse-Response or FIR
systems). Our simple resonator
theoretically continues vibrating for ever, so is an IIR system.
To
describe an LTI system algorithmically, we need a formulation of its behaviour
that allows both finite and infinite impulse responses. We do this by noting that the
characteristics of an LTI system must be expressed in a constant linear
relationship between previous output samples and previous input samples. That is, given input samples x[] and output
samples y[], some linear combination of output samples is related to some
linear combination of input samples:
|
|
This
is the general difference equation of an LTI system. It defines the behaviour of an LTI system in terms of a set of
coefficients a[0..p] that operate on current and previous input samples, and a
set of coefficients b[1..q] that operate on previous output samples. b[0] is always taken as 1. This is perhaps easier to see with this
reformulation:
![]()
This
can be readily implemented as a computer algorithm.
The
general difference equation leads to a simple classification of LTI systems:
(i) systems
with the coefficients b[1..q] are zero, in which case output samples are
generated by a linear combination of previous input samples. These are called non-recursive or moving
average systems.
(ii) systems
in which a[0] is 1, and a[1..p] are zero, in which case the output is formed
from a single input and a linear combination of past output samples. These are called simply recursive or autoregressive
systems.
(iii) systems
with arbitrary a[] and b[] coefficients are sometimes called autoregressive/moving average or ARMA systems. They are of course also recursive.
The
direct form implementation of the
general difference equation requires two memory arrays: one for past inputs x[]
and one for past outputs y[]. It can be
shown that the same result can be achieved with only a single memory of an
'internal' waveform s[]. This direct form II is the basis for the LTISystem() implementation below.
From
the description of an LTI system in terms of a[] and b[] coefficients we can
also determine its frequency response characteristics (note that we leave to
Unit 7 the reverse problem of the determination of a[] and b[] from the
frequency response). This is normally
performed using a mathematical transformation of the a[] and b[] coefficients
akin to the discrete Fourier transform, called the Z transform.
Put
simply, the Z transform converts a sequence of digital samples at successive
sampling instants to a polynomial of some operator z-1, in which the
amplitudes of the samples become the coefficients of the polynomial. Thus a finite signal x[1..n] has a Z
transform:
![]()
that is
![]()
One way of thinking of z-1 is that it
represents a unit delay. In other words multiplying by z-n delays a
z-transformed signal by n
samples. This analogy allows to view a
z-transformed signal as scaled impulses delayed appropriately and added
together.
The
conversion of a sequence to a polynomial is useful because it allows us to
write the general difference equation as two polynomials:
|
|
Where
X(z) is the z-transform of the input x[], and Y(z) the z-transform of the
output y[]. The cross multiplication
and collection of terms in z-n is equivalent to convolution on the
original signals. This polynomial form
of the difference equation allows us to form the response of the system:
|
|
that
is, as a ratio of two polynomials in z.
We can then see that this response will have peaks at the roots[1]
of the denominator polynomial - these are called the poles of the system, and dips at the roots of the numerator
polynomial - these are called the zeros
of the system. Our LTI system can be
described completely (with the addition of an overall gain factor) by the
location of the poles and zeros of the system.
These will in general be complex numbers and can be plotted on the
complex plane on a diagram called a z-plane
diagram.
To
obtain the frequency response of our system we need to put into the system
sinewaves at different frequencies but of unit amplitude and plot the output
amplitude. We do this by substituting z-1
in our polynomial for the complex sine eiW where W is the angular frequency
(= 2πf/Fs) at which we require the response. We can now obtain a numerical value for the response
for a range of frequencies between 0 and the sampling rate (2p). What we are
actually calculating is the product of the distances between each system zero
and a point on the unit circle
specified by eiW divided by the product
of the distances between each pole and that point. Thus the nearer the poles are to the unit circle the higher the
peaks in the response and the closer the zeros are to the unit circle the lower
the dips. The magnitude of this ratio
at a given frequency is the magnitude of the frequency response, while the
argument of this ratio is the phase response.
Algorithms
Algorithm
4.1 Convolution
|
// conv.cpp -- implementation of Convolution of 2 waveforms // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "conv.h" // The function Convolve performs convolution of two // time domain waveforms Waveform Convolve( const Waveform& x, // input waveform const Waveform& h // impulse response ) // returns convolved sequence { Waveform y(x.count(),x.rate()); // for each output sample for (int n=1;n<=y.count();n++) { y[n] = 0; // sum of product with reverse IR for (int k=0;k<h.count();k++) y[n] += x[n-k] * h[k+1]; // exploits bad index capability of x[] } return y; } |
Algorithm 4.2 Linear time-invariant
system model
|
// ltisys.h -- definition for Linear system class // // C++ (c) 1996 Mark Huckvale University College London // The LTISystem class provides a convenient implementation // of a linear time-invariant system including estimation // of frequency response #ifndef _LTISys_H #define _LTISys_H #include "wavedoub.h" #include "complex.h" class LTISystem { public: // public for demonstration purposes WaveDouble a; // numerator WaveDouble b; // denominator WaveDouble s; // state memory public: // constructors LTISystem(int na,int nb); LTISystem(const LTISystem& ltis); ~LTISystem(); // assignment LTISystem& operator= (const LTISystem& ltis); // clear system void clear(); // run system double operator() (double ival); // frequency response Complex response(double freq) const; }; #endif |
|
// ltisys.cpp -- implementation for Linear system class // // C++ (c) 1996 Mark Huckvale University College London // The LTISystem class provides a convenient implementation // of a linear time-invariant system including estimation // of frequency response #include "tools.h" #include "ltisys.h" // constructors LTISystem::LTISystem(int na,int nb) : a(na+1,1,0), // a[0]..a[na] b(nb+1,1,0), // b[0]..b[nb] (but b[0]=1.0) s((na>nb)?na+1:nb+1,1,0) // s[0]..s[max(na,nb)] { clear(); } LTISystem::LTISystem(const LTISystem& ltis) { a = ltis.a; b = ltis.b; s = ltis.s; } LTISystem::~LTISystem() { } // assignment LTISystem& LTISystem::operator= (const LTISystem& ltis) { if (this == <is) return *this; a = ltis.a; b = ltis.b; s = ltis.s; return *this; } // clear void LTISystem::clear() { for (int i=0;i<s.count();i++) s[i]=0; } // run sample through system double LTISystem::operator() (double ival) { int i; // shift state memory for (i=s.count()-1;i>0;i--) s[i] = s[i-1]; // compute s[0] from y[] coefficients s[0] = ival; for (i=1;i<b.count();i++) s[0] -= b[i] *s[i]; // compute output from x[] coefficients double out = 0; for (i=0;i<a.count();i++) out += a[i] * s[i]; return out; } |
Algorithm 4.3 LTI System response
|
// calculate frequency response Complex LTISystem::response(double freq) const { int i; WaveComplex omega(s.count(),1,0); Complex z=exp(Complex(0,2*PI*freq)); // initialise polynomial of complex frequency omega[0] = 1.0; omega[1] = z; for (i=2;i<s.count();i++) omega[i] = omega[i-1] * z; // compute response of numerator Complex rnum(0,0); for (i=0;i<a.count();i++) rnum += a[i] * omega[i]; // compute response of denominator Complex rden=omega[0]; for (i=1;i<b.count();i++) rden += b[i] * omega[i]; // compute ratio if (mag(rden)==0) return 1.0E5; // i.e. infinity else return rnum/rden; } |
Algorithm 4.4 Digital resonator
A mathematical
justification for the formula used to build a digital resonator is also
available.
|
// reson.cpp -- implementation of simple digital resonator // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "ltisys.h" #include "reson.h" // The Resonator function sets up a linear system consisting // of a complex pole pair LTISystem Resonator( double freq, // natural frequency // (fraction of sample rate) double bwid // bandwidth // (fraction of sampling rate) ) // returns linear system { LTISystem ltis(0,2); // get parameters as angles double wf = 2*PI*freq; double wb = 2*PI*bwid; // estimate pole radius from bandwidth // (rule of thumb) double r = 1.0 - wb/2; // set up numerator ltis.a[0] = 1.0; // set up denominator: quadratic formula ltis.b[1] = -2.0 * r * cos(wf); ltis.b[2] = r * r; // adjust numerator for unity gain at DC ltis.a[0] /= mag(ltis.response(0)); return ltis; } |
Bibliography
Meade & Dillon, Signals and
Systems, Chapter 5.
Lynn & Fuerst, Introductory Digital Signal
Processing, Chapters 2 & 4.
Orfanidis, Introduction to Signal
Processing, Sections 5.1, 5.4, 6.1-6.3.
Example Programs
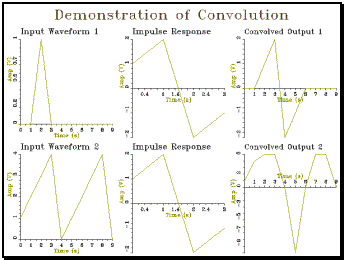
Example 4.1 Demonstration of convolution
|
// conv_t.cpp -- demonstration of convolution #include "tools.h" #include "conv.h" int main() { int i; Graph gr(2,3,"Demonstration of Convolution"); // create input signal and display Waveform x(10,1); for (i=1;i<=10;i++) x[i]=0; x[3]=1; x.plot(gr,1,"Input Waveform 1"); // create impulse response Waveform h(4,1); h[1]=1; h[2]=2; h[3]=-2; h[4]=-1; h.plot(gr,2,"Impulse Response"); // do convolution Waveform y = Convolve(x,h); y.plot(gr,3,"Convolved Output 1"); // try a different input for (i=1;i<=10;i++) x[i]=i%5; x.plot(gr,4,"Input Waveform 2"); // same impulse response h.plot(gr,5,"Impulse Response"); // do convolution y = Convolve(x,h); y.plot(gr,6,"Convolved Output 2");
gr.close(); } |
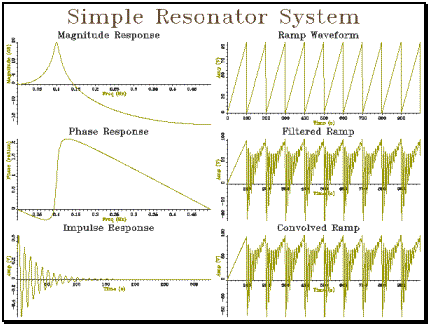
Example 4.2 Equivalence of filtering and convolution
|
// reson_t.cpp -- demonstration of resonator design & convolution #include "tools.h" #include "conv.h" #include "ltisys.h" #include "reson.h" const double ILIMIT=1.0E-5; // length limit for impulse response int main() { int i; Graph gr(3,2,"Simple Resonator System"); // create resonator LTISystem ltis=Resonator(0.1,0.01); // calculate frequency response Spectrum fresp(500,1000); for (i=0;i<500;i++) fresp[i] = ltis.response(i/1000.0); fresp.plotLogMag(gr,1,"Magnitude Response"); fresp.plotPhase(gr,3,"Phase Response"); // calculate impulse response Waveform iresp(0,1); double lval = 0; // last output double oval = ltis(1.0); // put in unit pulse while ((fabs(oval) > ILIMIT) || (fabs(oval-lval) > ILIMIT)) { iresp += oval; // append sample lval = oval; // remember sample oval = ltis(0.0); // get next sample } iresp.plot(gr,5,"Impulse Response"); // create a ramp waveform Waveform ramp(1000,1); for (i=1;i<=1000;i++) ramp[i] = i % 100; ramp.plot(gr,2,"Ramp Waveform"); // filter a ramp waveform Waveform framp(1000,1); ltis.clear(); for (i=1;i<=1000;i++) framp[i] = ltis(ramp[i]); framp.plot(gr,4,"Filtered Ramp"); // convolve ramp with impulse response Waveform cramp=Convolve(ramp,iresp); cramp.plot(gr,6,"Convolved Ramp"); gr.close(); } |
Exercises
4.1 Explain the first three values of
'Convolved Output 2' (they are: 1, 4 & 5).
4.2 Modify example program 4.1 so that the
impulse response is a square wave.
4.3 Modify example program 4.1 so that the
impulse response matches the input waveform in each case.
4.4 Adapt example program 4.2 to send a stream of pulses through the resonator rather than the ramp wave, displaying the input and output signals.
4.5 Adapt example program 4.2 to generate the output from a resonator with a natural frequency of 25Hz and a bandwidth of 7.5Hz when fed with a pulse train at 10Hz lasting 1 second and sampled at 1,000Hz. Display the result. (Hint: create a Signal of 1000 samples at 1000 samples/sec, create a Resonator of centre frequency (25/1000) and bandwidth (7.5/1000), then run the resonator into the signal, putting in pulses every 100 samples)