Construction
of a Digital Resonator
1.
z-plane description
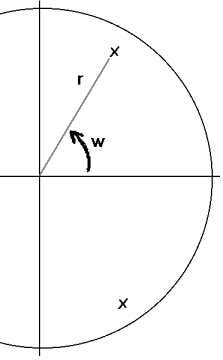
A digital resonator is a recursive (IIR) linear system
having a complex conjugate pair of poles located inside the unit circle of the
z-plane.
The angle of the poles in polar co-ordinates sets the
resonant frequency of the resonator, while the distance of the poles are to the
unit circle sets the bandwidth. The
closer they are to the unit circle, the smaller the bandwidth.
We first seek an expression for the z-plane location of the
poles, then expand the expression for the linear system to obtain the b[]
coefficients.
2.
Pole location
|
|
|
|
Angle to pole, w = 2pf where f is resonant
frequency expressed as fraction of sampling rate.
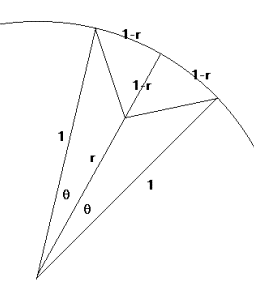
To find r from bandwidth, find the 3dB points on unit
circle. These need to be Ö2
further away from the pole than the unit circle.
|
|
Therefore have triangles of sides (1-r), (1-r) and Ö2(1-r)
between pole and 3dB points.
We can then see that:
sin(q) = 1
- r
and since q is small and equal to half the bandwidth:
r » 1 -
b/2
where b is bandwidth expressed in radians.
3.
Form difference equation
Poles are at r(cos(w)+isin(w))
and r(cos(w)-isin(w)).
So H(z) =
1/(1-r(cos(w)+isin(w))z-1)(1-r(cos(w)-isin(w))z-1)
Expanding:
H(z) = 1/(1 - 2rcos(w)z-1 +
r2z-2)
Therefore coefficients are:
a0 = 1
b0 = 1
b1 =
-2rcos(w)
b2 = r2
MAH
8Nov97