
UNIT
5:
DISCRETE
FOURIER
TRANSFORM
Summary
††††††††††† This
unit introduces the Discrete Fourier Transform as a means for obtaining a
frequency based representation of a digital signal.† The special characteristics of the Fast Fourier Transform implementation
are described.
††††††††††† When you have worked through this unit you should:
∑
be able to explain what information is represented on a magnitude
spectrum and on a phase spectrum of a discrete signal
∑
be able to state the mathematical expression for the Discrete-time
discrete-frequency Fourier Transform (DFT)
∑
understand how the direct implementation of the DFT operates
∑
appreciate that the direct implementation of the DFT is very
inefficient, and that the Fast discrete-time discrete-frequency Fourier Transform
(FFT) provides a more efficient means of its calculation
∑
have a qualitative understanding of the operation of the
decimation-in-time form of the FFT
∑
be able to predict how simple sine and cosine signals appear on the DFT
in the region from 0 to Fs.
Concepts
††††††††††† A
digital signal of finite duration x[1..N] can be specified in the time domain
as a sequence of N scaled impulses occurring at regular sampling instants: each
impulse taking on the amplitude of the signal at that instant.† The same signal may also be described as a
combination of N complex sinusoidal components X[0..N-1], each of a given
frequency and phase, and each being a harmonic of the sampling rate/N.† This representation, called a
frequency-domain representation, may be obtained from the time-domain form
through the use of the Discrete Fourier
Transform or DFT.† The time domain form and the frequency
domain form are simply different ways of representing the same digital signal,
one is chosen over the other simply in terms of utility for a given purpose.
††††††††††† The
Discrete Fourier Transform X(f) of a signal x[1..N] is defined as:
|
††††††††††††††††††††††††††††††††††††††††††††††††
|
††††††††††† where X[k] is the amplitude of the kth
harmonic, where k varies from 0 to N-1 and where k/N represents a fractional
frequency value of the sampling rate.†
In general X[] and x[] can hold complex values, and X[] will be complex
even if x[] is purely real.
††††††††††† The
graph of |X(f)| against frequency is known as the magnitude spectrum.† The graph
of arg X(f) against frequency is known as the phase spectrum.
††††††††††† By
copying a real digital signal into a complex sequence x[1..N], the DFT has a
straightforward algorithmic implementation (shown in
ComplexDFT()), using complex multiplication with the complex
exponential defined as:
|
††††††††††††††††††††††††††††††††††††††††††††††††††
|
††††††††††† and
hence:
|
††††††††††††††††††††††††††††††††††††††††††††
|
††††††††††† We
can also define the inverse transform, from the frequency representation X[] back
to the time representation x[]:
|
††††††††††††††††††††††††††††††††††††††††††††††††††††
|
††††††††††† where
n varies from 1 to N.† We have chosen to
place the scaling factor 1/N in the forward transform, but many authorities
place it in the inverse transform.† We choose
to place it here because it leads to harmonic amplitudes which are normalised
to the sequence length, and hence independent of the amount of signal
analysed.† This leads naturally to an
equivalence between the energy in the signal and the energy in the spectrum:
|
†††††††††††††††††††††††††††††††††††
|
††††††††††† The
frequency spectrum is often displayed in log magnitude terms in units of decibels (dB), and may be converted
using:
|
†††††††††††††††††††††††††††††††
|
††††††††††† From a
real signal at a sampling rate Fs, the DFT provides N harmonic
amplitudes at frequencies from 0 to ![]() .† However the
frequencies from 0 to Fs/2 are aliased to the region Fs/2
to Fs, so only the lower N/2 amplitudes are important.
.† However the
frequencies from 0 to Fs/2 are aliased to the region Fs/2
to Fs, so only the lower N/2 amplitudes are important.
††††††††††† The
phase angles may be converted to degrees using:
|
††††††††††††††††††††††††††††††††††††††††††††††††††††††
|
††††††††††† The
Fast Fourier Transform or FFT is simply a particular
implementation of the DFT, that gives identical results, but which takes considerably
less calculation.† It does this by
eliminating a great deal of redundant computation in the DFT in the
circumstances when the sequence length N is a power of 2 (i.e. 4, 8, 16, 32,
64, etc).
††††††††††† In
a normal DFT, each harmonic amplitude is the result of N complex multiplies
with N different complex exponentials - giving a total of N2
multiplies for all N harmonics.† When N
is a power of 2, many of these multiplies concern identical numerical multiplicands
and many of the complex exponentials are zero or 1.† When redundant computation is removed, the number of multiplies
is Nlog2(N) rather than N2 and this represents a very
large saving when N is large (e.g. for 1024 samples there is 100 times less
calculation).
††††††††††† At
the heart of the FFT is a simple algebraic manipulation that takes two input
values, performs a multiply operation with a complex exponential and produces
two output values.† This basic unit is
called a 'butterfly', and for two complex inputs a and b, a frequency W
(=2πkn/N), and outputs p and q, the butterfly calculation is
|
††††††††††††††††††††††††††††††††††††††††††††††
|
††††††††††† We
shall diagram this basic operation as:
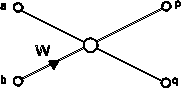 1
1
††††††††††† This
actually represents the DFT of a 2 sample waveform.† Longer waveforms can be processed by combining these butterfly
operations with variations on the value of W.†
Thus a DFT of an 8 sample waveform x[0] to x[7] can be graphed as:
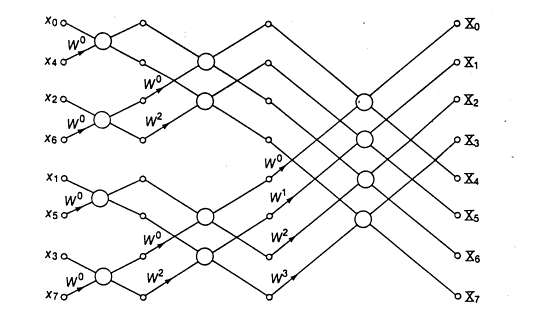
††††††††††† Where
Wj is one of the frequencies in the DFT calculation (=2πj/N).
This signal flow graph is the basis
of the ComplexFFT() implementation.† To operate the graph, the input signal is shuffled into the
spectrum array in an order known as bit-reversed
addressing.† Then each column of
butterfly operations is performed, so that the signal 'moves' left-to-right
through the graph, turning into the DFT spectrum.
††††††††††† A more mathematical explanation
of the FFT is also available.
Implementation Note
††††††††††† The
FFT routines have not been written for maximum efficiency.† Note that the calculation of the
bit-reversed addresses and the values of the complex exponentials need only be
performed once for a given size of transform.†
Since typical use of the FFT is the repeated use of the transform on
constant lengths of waveform,† these
tables may be pre-calculated and stored.
Bibliography
††††††††††† Meade & Dillon, Signals and Systems, Chapter
7, pp130-144.
††††††††††† Lynn
& Fuerst, Introductory Digital Signal Processing, Chapter 7.
††††††††††† Orfanidis, Introductory Signal Processing, Chapter
9.
Algorithms
††††††††††† Algorithm 5.1 Complex to Complex
Discrete Fourier Transform
|
|
|
// cdft.cpp -- complex-to-complex Discrete Fourier Transform // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "cdft.h" // The ComplexDFT function implements a general complex to // complex discrete fourier transform Spectrum ComplexDFT(const ComplexWaveform& x) { †††††† Spectrum s(x.count(),x.count()/x.rate()); †††††† // for each output harmonic †††††† for (int i=0;i<x.count();i++) { ††††††††††††† // get frequency ††††††††††††† double f = (2 * PI * i) / x.count(); ††††††††††††† // compute complex sum ††††††††††††† Complex sum=0.0; ††††††††††††† for (int j=0;j<x.count();j++) †††††††††††††††††††† sum += x[j+1] * exp(Complex(0.0,-f*j)); ††††††††††††† // scale ††††††††††††† s[i] = sum/x.count(); †††††† } †††††† return s; } // The ComplexIDFT function implements a general complex to // complex inverse discrete fourier transform ComplexWaveform ComplexIDFT(const Spectrum& s) { †††††† ComplexWaveform x(s.count(),s.count()/s.rate()); †††††† // for each output sample †††††† for (int i=0;i<x.count();i++) { ††††††††††††† // get frequency ††††††††††††† double f = (2 * PI * i) / x.count(); ††††††††††††† // compute complex sum ††††††††††††† Complex sum=0.0; ††††††††††††† for (int j=0;j<x.count();j++) †††††††††††††††††††† sum += s[j] * exp(Complex(0.0,f*j)); ††††††††††††† x[i+1] = sum; †††††† } †††††† return x; } |
††††††††††† Algorithm
5.2† Complex Fast Fourier Transform
|
// cfft.cpp -- implementation of complex-to-complex Fast Fourier Transform // // C++ (c) 1996 Mark Huckvale University College London #include "tools.h" #include "cfft.h" // The iLog2 function returns the integer log based 2 int††† iLog2(int x) { †††††† int††† p=0; †††††† int††† y=1; †††††† while (y < x) { ††††††††††††† p++; ††††††††††††† y *= 2; †††††† } †††††† return p; } // The iPow2 function returns the integer power of 2 int††† iPow2(int p) { †††††† int††† x=1; †††††† while (p > 0) { ††††††††††††† p--; ††††††††††††† x *= 2; †††††† } †††††† return x; } // The FFTBitReverseTable function returns a dynamically-allocated // table of indexes for FFT in-place sample shuffling int *† FFTBitReverseTable(int size) { †††††† int††† *idx = new int[size]; †††††† // find # bits involved †††††† int††† nbit = iLog2(size); †††††† // for each table entry †††††† for (int i=0;i<size;i++) { ††††††††††††† // store bit reversed index ††††††††††††† int a1 = i; ††††††††††††† int a2 = 0; ††††††††††††† for (int j=1;j<=nbit;j++) { †††††††††††††††††††† a2 *= 2; †††††††††††††††††††† if (a1 & 1) a2 |= 1; †††††††††††††††††††† a1 /= 2; ††††††††††††† } ††††††††††††† idx[i] = a2; †††††† } †††††† return idx; } // The FFTButterfly function performs the key FFT cross-multiply void FFTButterfly(Complex& upper,Complex& lower,const Complex& w) { †††††† Complex temp = lower * w; †††††† lower = upper - temp; †††††† upper = upper + temp; } |
|
// The ComplexFFT function implements a fast complex to // complex discrete fourier transform Spectrum ComplexFFT(const ComplexWaveform& x) { †††††† int††† size = iPow2(iLog2(x.count())); †††††† Spectrum s(size,size/x.rate()); †††††† // get bit reverse table †††††† int *amap = FFTBitReverseTable(size); †††††† // shuffle input data into spectrum †††††† for (int i = 0 ; i < size ; i++) ††††††††††††† s[amap[i]] = x[i+1]; ††††††††††††† // uses bad index capability of x[] †††††† // do multiple butterfy passes over data †††††† //†† with steps of 1,2,4,..,N †††††† for (int d = 1 ; d < size ; d *= 2) { ††††††††††††† // for each start position ††††††††††††† for (int j = 0 ; j < d ; j++) { †††††††††††††††††††† Complex w = exp(Complex(0,-(PI*j)/d)); †††††††††††††††††††† // for each step †††††††††††††††††††† for (int i = j ; i < size ; i += 2*d) †††††††††††††††††††††††††† // do butterfly †††††††††††††††††††††††††† FFTButterfly(s[i],s[i+d],w); ††††††††††††† } †††††† } †††††† // normalise †††††† for (int i = 0 ; i < size ; i++) ††††††††††††† s[i] /= x.count(); †††††† delete [] amap; †††††† return s; } // The ComplexIFFT function implements a fast complex to // complex inverse discrete fourier transform ComplexWaveform ComplexIFFT(const Spectrum& s) { †††††† ComplexWaveform x(s.count(),s.count()/s.rate()); †††††† // get bit reverse table †††††† int *amap = FFTBitReverseTable(x.count()); †††††† // shuffle input data into waveform †††††† for (int i = 0 ; i < s.count() ; i++) ††††††††††††† x[i+1] = s[amap[i]]; †††††† // do multiple butterfy passes over data †††††† //†† with steps of 1,2,4,..,N †††††† for (int d = 1 ; d < s.count() ; d *= 2) { ††††††††††††† // for each start position ††††††††††††† for (int j = 0 ; j < d ; j++) { †††††††††††††††††††† Complex w = exp(Complex(0,(PI*j)/d)); †††††††††††††††††††† // for each step †††††††††††††††††††† for (int i = j+1 ; i <= s.count() ; i += 2*d) †††††††††††††††††††††††††† // do butterfly †††††††††††††††††††††††††† FFTButterfly(x[i],x[i+d],w); ††††††††††††† } †††††† } †††††† delete [] amap; †††††† return x; } |
Example Programs
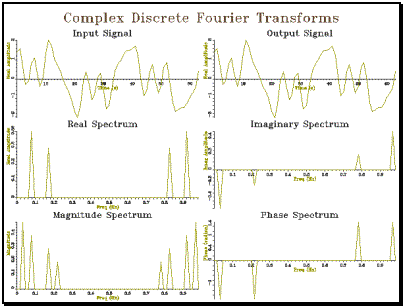
††††††††††† Example
5.1 Complex Discrete Fourier Transform
|
// cdft_cpp -- demonstration of Complex DFT & IDFT #include "tools.h" #include "cdft.h" const int SIZE=64; int main() { †††††† int††† i; †††††† // create a test signal †††††† ComplexWaveform ip(SIZE,1); †††††† for (i=1;i<=SIZE;i++) { ††††††††††††† double f = 2 * PI * (i-1) / SIZE; ††††††††††††† ip[i] = Complex(1.0 * sin( 2*f) + †††††††††††††††††††††††††† † 0.8 * cos( 5*f) + †††††††††††††††††††††††††† † 0.6 * cos(11*f) + †††††††††††††††††††††††††† † 0.4 * sin(14*f), †††††††††††††††††††††††††† † 0); †††††† } †††††† // generate spectrum †††††† Spectrum s=ComplexDFT(ip); †††††† // generate signal again †††††† ComplexWaveform op=ComplexIDFT(s); †††††† // plot as graphs †††††† Graph gr(3,2,"Complex Discrete Fourier Transforms"); †††††† ip.plotReal(gr,1,"Input Signal"); †††††† op.plotReal(gr,2,"Output Signal"); †††††† s.plotReal(gr,3,"Real Spectrum"); †††††† s.plotImag(gr,4,"Imaginary Spectrum"); †††††† s.plotMag(gr,5,"Magnitude Spectrum"); †††††† s.plotPhase(gr,6,"Phase Spectrum"); †††††† gr.close(); } |
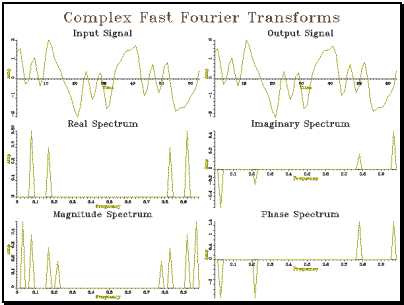
††††††††††† Example
5.2 Complex Fast Fourier Transform
|
// cfft_cpp -- demonstration of Complex FFT & IFFT #include <iostream.h> #include "tools.h" #include "cfft.h" const int SIZE=64; int main() { †††††† int††† i; †††††† // create a test signal †††††† ComplexWaveform ip(SIZE,1); †††††† for (i=1;i<=SIZE;i++) { ††††††††††††† double f = 2 * PI * (i-1) / SIZE; ††††††††††††† ip[i] = Complex(1.0 * sin( 2*f) + †††††††††††††††††††††††††† † 0.8 * cos( 5*f) + †††††††††††††††††††††††††† † 0.6 * cos(11*f) + †††††††††††††††††††††††††† † 0.4 * sin(14*f), †††††††††††††††††††††††††† † 0); †††††† } †††††† // generate spectrum †††††† Spectrum s=ComplexFFT(ip); †††††† // generate signal again †††††† ComplexWaveform op=ComplexIFFT(s); †††††† // plot as graphs †††††† Graph gr(3,2,"Complex Fast Fourier Transforms"); †††††† ip.plotReal(gr,1,"Input Signal","Time","Amp"); †††††† op.plotReal(gr,2,"Output Signal","Time","Amp"); †††††† s.plotReal(gr,3,"Real Spectrum","Frequency","Amp"); †††††† s.plotImag(gr,4,"Imaginary Spectrum","Frequency","Amp"); †††††† s.plotMag(gr,5,"Magnitude Spectrum","Frequency","Amp"); †††††† s.plotPhase(gr,6,"Phase Spectrum","Frequency","Amp"); †††††† gr.close(); } |
Exercises
5.1†††††† The inverse DFT provides a simpler method to synthesize a
square wave: set up the spectrum of a square wave and call ComplexIDFT().† Set up a spectrum as follows:
††††††††††††††††††††††† Spectrum(1000,0.05);†††††††† // 0..19,980Hz in 1000 steps
†††† Then put in the odd harmonics of 100Hz with
appropriate amplitudes (amplitude of nth
harmonic is just 1/n).† That is, put in
amplitudes of 1.0 at spectrum position 5, 0.33 at position 15, 0.2 at position
25, etc.† Donít forget to put in the
mirror images at positions 995, 985, 975, etc.†
Plot your spectrum and the result of the inverse DFT.
††††††††††† How would you change your solution
to use an FFT?† Why might you want to?
5.2†††††† Modify Examples 5.1 and 5.2 to explore the differences between
an exact DFT of a 40 point test waveform and the FFT of the same waveform
suffixed with 24 zeros.† Plot a graph
showing the magnitude spectrum and the phase spectrum of the same signal
analysed in these two ways.
††††††††††† What differences are there between an FFT of a 64 point waveform and an FFT of the same waveform appended with 64 zeros?