Basis
of the Fast Fourier Transform
1.
Basic equation
We shall take as the basic relationship
of the discrete Fourier Transform:
![]()
where X[k] is the kth
harmonic (k=0..N-1), x[n] is the nth input sample (n=0..N-1), and WN
is shorthand for exp(-i2p/N). This is a slight simplification of the
formula in the notes for purposes of exposition.
2.
The 2 point transform
When N=2, we can write out the formulae
for the harmonics as:
![]()
![]()
but, ![]() = 1 and
= 1 and ![]() = exp(-ip)
= -1. So this can be re-written as:
= exp(-ip)
= -1. So this can be re-written as:
![]()
![]()
The 2 point transform is very easy to
compute! It takes just one addition and
one subtraction.
3.
Decimation in time
What we aim to do is to simplify the
expression for a transform of length N by re-writing it as the combination of
two transforms of length N/2. Here we
use the procedure called decimation in time.
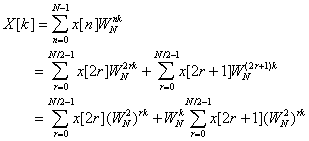
Here, we decompose the operations on
x[] into the sum of operations on the even samples of x[] and the odd samples
of x[]. In the next line, we rewrite
the sum to involve the exponential terms ![]() rather than
rather than ![]() . Now use the important
equality:
. Now use the important
equality:
![]()
to show that the division into two
sub-sequences gives the same result (apart from a ‘twiddle factor’) as the sum
of two transforms of length M=N/2:
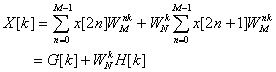
Where G[k] and H[k] are transforms of
half the original size. If N is a
multiple of 4, then the decomposition can be applied again to into the sum of 4
transforms of length N/4. If N is a
power of 2, then we can perform log2N decomposition stages into the
sum of N/2 transforms of length 2. And we
have already noted that transforms of length 2 are very simple to implement.
4.
Signal flow graph realisation
If we study the set of equations for a
transform of some length N which is a power of 2, we find that the values of
the WN factors take on a small range of values, many of which are ±1
or ±i.
These terms can be implemented without multiplication. In addition, many of the products of x[n]
with these terms arise many times, and hence need only be calculated once.
The combination of the ideas of (i) the
simplicity of the 2 point transform, (ii) the decimation in time of a transform
of length N into transforms of length 2, and (iii) the removal of unnecessary
multiplication, produces a DFT procedure that is substantially more efficient.
Let us implement a transform of length
4 in an efficient way using these ideas.
The procedure could be applied to any transform of length 2M.
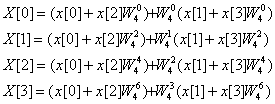
but note that ![]() is the same as
is the same as ![]() , and
, and ![]() is the same as
is the same as ![]() , so the last two harmonics can be written as:
, so the last two harmonics can be written as:
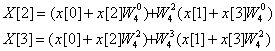
We can now see that some of the
two-point transforms are shared between the harmonics and so only need to be
calculated once. We can demonstrate
this in a signal flow diagram such as the one below:
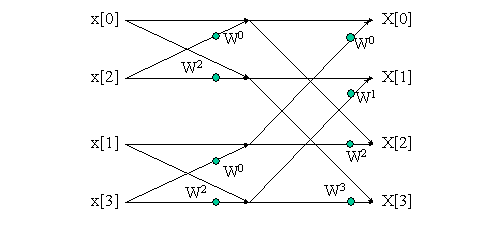
The diagram shows two processing
stages. In stage 1, four intermediate
values are calculated:
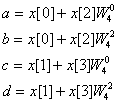
Then in stage 2, these values are
combined to give the final results:
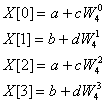
5.
Performance improvements
The basic DFT formula requires N
complex multiplications for each of N harmonics, making N2
multiplications in total. In the
decimation in time procedure and the signal flow graph, there are log2N
processing stages, each of N complex multiplications, or Nlog2N
multiplications in total. The
difference is large for reasonable N:
|
N |
N2 |
Nlog2N |
Ratio |
|
8 |
64 |
24 |
2.7 |
|
64 |
4096 |
384 |
10.7 |
|
512 |
262144 |
4608 |
56.9 |
|
4096 |
16777216 |
49152 |
341.3 |