

Abstract
This study investigates the correlations between phonetic, perceptual
and auditory properties of fricatives through the use of spatial
representations as opposed to a more conventional characterisation
with multiple interacting acoustic cues. These are constructed
from estimated distances between fricatives in each domain. A
variety of fricative and fricative-like stimuli were examined.
Perceptual distances were derived from subjective judgements of
the similarities between the fricatives. Auditory distances were
obtained from critical bandpass filter banks and distance metrics
were applied to model the spectral processing in the auditory
periphery. The distances in the perceptual and auditory spaces
were analysed using multidimensional scaling in order to test
their correlation and how it varied according to the naturalness
of the stimulus materials. Quantitative measures
of the relations between the spaces were given by canonical correlation
analyses. The results show that the perception of fricative segments
may be explained in terms of 2-dimensional auditory space in which
each segment occupies a region. The dimensions of the space were
found to be the frequency of the main spectral peak and the 'peakiness'
of spectra. These results support the view that perception of
a segment is based on its occupancy of a multidimensional parameter
space. This view is also consistent with models of speech perception
such as the prototype theory (Kuhl, 1995).
1. Introduction
This study attempts to investigate the relationships between the
acoustic and perceptual properties of fricatives and their linguistic
classification.
Traditional approaches to such investigations have been based on the perceptual testing of acoustic cues hypothesised to be responsible for each phonetic contrast. Such studies have made significant progress in understanding the detailed structure of acoustic signals, but at the same time produce perceptual models which show great complexity in cue interaction associated with any contrast.
Instead, this study concentrates on similarity data, which can be used to build spatial models of each level of perceptual processing acoustic signals, perceptual judgements, and phonetic contrasts. At each level of representation, a spatial map is used to indicate the relative location of units on dimensions where distance is inversely related to the similarity.
This approach is built on the hypothesis that phonetic units are recognised in terms of regions they occupy in such spaces with respect to the other units. The axes of this space are determined by the measurements we make of a segment in each level of perceptual description and a point in this space is a combination of a set of these measurements over a given time interval. This approach is consistent with models of speech perception such as the prototype theory, according to which the correct identification of speech segments depend on the perceived distances between speech stimuli and a prototype/region in perceptual space (Kuhl, 1995). Under this hypothesis, the segment /b/ would not be recognised by extraction of a set of relevant acoustic cues, such as voicing or bilabial burst frequency, but simply by the proximity of the sound to regions or prototypes in the measurement spaces. Cue interactions, it is hypothesised, would simply fall out as a consequence of the similarity measure.
These similarity-based approaches are justified if there is a close correspondence between spatial representations at acoustic, perceptual, and phonetic levels (after appropriate acoustic metric analysis), and this provides evidence that the perceptual system could be operating in a very simple way; matching inputs to prototypes/regions with a similarity measure based on general characteristics of the speech signal. Conversely, if there is no match or poor match between these spaces, this implies that some other process is involved, for example; the acoustic metric may be inadequate, the primary auditory analysis (input) may be inappropriate or there may be some other perceptual influence.
Early examples of studies based on such an approach are by Pols et al. (1969) and Klein et al. (1970) on vowel sounds. These works show how the acoustic/auditory space could be directly and quantitatively related to the perceptual space, which was in turn closely matched to the phonetic structure. To enable this, first two domains need to be quantified.
In the auditory domain, measurements were the outputs in decibels in the 18 frequency channels from a spectral slice of each 11 vowels. Consequently, these measurements can be modelled as 11 points in an 18-dimensional physical space. However, they showed that the data points can be reduced to a few principal physical components (dimensions) without much loss of the physical variance in the data. They used the Principal Component Analysis (PCA; Harman, 1967) for this purpose and managed to model the physical measurements in a three-dimensional physical space. Note that this method of obtaining acoustic space does not specifically refer to 'well-defined' formants, so that it can be applied to the analysis of any sound spectra.
The perceptual measurements were taken from similarity judgements of these vowels; listeners were just asked to choose the most similar sounding pair of vowels out of a set of three. The perceptual dimensions revealed from Multidimensional Scaling (MDS; Kruskal, 1964) analysis of the similarity judgements were also closely related to the dimensions of the auditory measurement spaces. They also showed that these dimensions are closely matched to configurations on phonetic/articulatory space, the main axes being frontness and height, as well as the acoustic dimensions of vowel formant measurements.
However, the Pols et al. study contained a serious flaw in the quality of the vowel stimuli which were artificial to the extent that they sounded more like complex synthetic signals than vowels. Subsequently, the results had to be verified using natural vowel segments (in Klein et al.) This suggests that, for present study, we need to be careful about the nature of the stimuli, if we are to make any claims about mechanisms involved in speech perception; we can predict that nonspeech sounds will give a high correlation between perceptual and auditory spaces, since there will certainly not be any phonetic influence in the perception of nonspeech sounds.
On the whole, approaches such as Pols et al. have not been applied to consonants. If, however, we suppose that consonants and vowels are subject to the same physiological and linguistic constrains, it may be worthwhile to formulate a comprehensive model of speech perception, both for vowels and consonants.
The aim is to illustrate the possibility of a spatial approach
to explanations of speech processing in consonant perception.
The question is: To what extent can perceptual similarities be
explained in terms of their spatial configurations in each level
of processing? Fricatives are used as convenient materials in
which the knowledge of vowel studies can be transferred to the
analysis of consonant sounds. The present study is loosely modelled
on Pols et al., but a pilot study on the English voiceless
fricatives 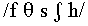 showed that, unlike vowels, consonant perception might
not be readily explained by their acoustic characteristics. This
result has led to the construction of four stimulus sets which
reflect a change in terms of their acoustic parameters from natural
speech to evidently synthetic versions. It is hypothesised that
the simpler the spectral patterns of stimulus sets, the higher
the correlation between their perceptual and auditory spaces,
thereby reflecting the simplicity and directness of the perceptual
processing involved. More complex spectral patterns are expected
to involve some kind of perceptual influence, indicated by the
lower correlation between the spaces.
showed that, unlike vowels, consonant perception might
not be readily explained by their acoustic characteristics. This
result has led to the construction of four stimulus sets which
reflect a change in terms of their acoustic parameters from natural
speech to evidently synthetic versions. It is hypothesised that
the simpler the spectral patterns of stimulus sets, the higher
the correlation between their perceptual and auditory spaces,
thereby reflecting the simplicity and directness of the perceptual
processing involved. More complex spectral patterns are expected
to involve some kind of perceptual influence, indicated by the
lower correlation between the spaces.
In addition, the principal components analysis has to be adapted to accommodate the dynamic characteristics of consonant materials. The analysis technique also incorporates more sophisticated distance metrics than the Euclidean metric used in the principal component analyses.
The next section discusses the design of the stimuli and measurement of the perceptual similarities. Detailed MDS analyses establish the spatial configurations of the perceptual data. Auditory modelling of the perceptual data is given in §3. §4 is about multiple speaker production tests where the general auditory spaces of fricatives are estimated and their acoustic correlates are also identified. A general discussion of the results of production, perception and auditory experiments is given in §5.
2. Perception tests
2.1 Design of stimuli
The initial stimuli were fricatives 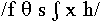 , read by a female English phonetician, a native
speaker of R.P., on a falling tone, followed by
, read by a female English phonetician, a native
speaker of R.P., on a falling tone, followed by 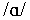 .
[x] was added to the usual English fricative set to increase the
number of combinations in similarity judgements. The materials
were recorded in an anechoic room onto a Sony DTC-1000ES digital
audio tape recorder. They were digitised with a 20 kHz sampling
frequency and 16-bit quantization, and transferred onto computer
disk. Fricatives were excised and normalised in their intensity
with respect to the RMS levels. From these initial stimuli, henceforth
referred to as natural stimuli, three additional stimulus
sets were devised. Thus, all stimuli consisted solely of voiceless
frication.
.
[x] was added to the usual English fricative set to increase the
number of combinations in similarity judgements. The materials
were recorded in an anechoic room onto a Sony DTC-1000ES digital
audio tape recorder. They were digitised with a 20 kHz sampling
frequency and 16-bit quantization, and transferred onto computer
disk. Fricatives were excised and normalised in their intensity
with respect to the RMS levels. From these initial stimuli, henceforth
referred to as natural stimuli, three additional stimulus
sets were devised. Thus, all stimuli consisted solely of voiceless
frication.
In the next stimulus set, the dynamic spectral properties were taken out, so that the stimuli have the same cross-sectional spectral shape throughout their whole length. This was done by LPC synthesis, modelled on the spectral cross-sections of the natural fricatives. The number of coefficients was set to 22 - this number was usually used to model vowel spectra by LPC, and most of the spectral characteristics which can be modelled by spectral peaks and valleys should be reflected in the spectral shape. The desired effect is like duplicating a period out of vowels many times to obtain static spectra (as in Pols et al., 1969). The length of stimuli was always set to 400 ms. These synthetic fricatives were also normalised with respect to overall RMS level. The stimuli in this set were called LPC22 stimuli.
The spectral shape of the fricatives was further simplified for the next stimulus set, LPC10. Here, 10 coefficients were used in an LPC analysis. The duration of the fricative portions was set to 400 ms and intensity normalised.
In the final stimulus set, fricative spectra are modelled by LPC with just four coefficients, so that the fricative spectrum is characterised by two peaks. These stimuli were called LPC4 stimuli. It has already been confirmed that the correlation between perceptual and auditory spaces for analogous nonspeech stimuli, consisting of only two spectral peaks and zeroes, is extremely high (Choo, 1996). If the result is otherwise for this stimulus set, it would imply something quite exclusive about speech perception. That is, there may exist perceptual processing mechanisms that incorporate factors other than the information contained in the acoustic signal.
A summary of the stimulus sets is given below:
For each stimulus set, an example of spectrograms and spectra of the stimuli are shown in Figures 1a-d.
| a. Natural set |
b. LPC22 set |
| c. LPC10 set |
d. LPC4 set |
Figure 1. The spectrograms and average cross-sectional
spectra of 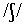 .
The spectra were obtained by FFT analyses of the marked regions
on the respective spectrograms.
.
The spectra were obtained by FFT analyses of the marked regions
on the respective spectrograms.
2.2 Subjects and procedure
First, each stimulus in each stimulus set was paired with two
other stimuli in the set, to make up a triad, ABC, which was in
turn paired to AB AC to help the short term memory of the listeners.
60 (= 6×5×4/2) triads were constructed for each set.
Two sets of stimuli were presented in each session. Half of the
stimuli were presented in the order AB AC while the other half
was presented in the order AC AB. The sequence of two pairs was
randomised for each presentation to take into account the ordering
effect.
These were recorded back to DAT tapes. There was 0.1 second of inter-stimulus and inter-stimulus-pair gap and 2 seconds pause after two pairs were presented. There was a pause of ten seconds after each block of 5 similarity judgement pairs. After that pause the listeners were prompted by a tone for the next block.
20 students, studying for a B.Sc. in Speech Science, were paid to listen to the stimuli. All were native speakers of English, and reported normal speech and hearing. Subjects were split into four groups and heard the stimulus sets in the order1 of natural set to LPC4 set. Subjects were tested five at a time in a sound treated room. Testing lasted for 30 minutes each session. After a short training session, the main experimental task consisted of listening to two sets of stimuli. Each test set began with the presentation of each of the stimuli once, followed by 5 trial pairs as practice. Each subject made judgements on a total of 240 stimuli over two days.
Similarity data were accumulated such that the pairs selected to be more similar were assigned scores of 1, and the pairs which were not selected scores of 0. In this way, a matrix of data indexing the perceived relationships among the six stimuli was obtained for each subject. An example of a subject's similarity matrix is given below for the natural stimulus set:
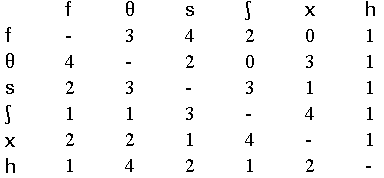
Table 1. Similarity matrix for a subject who rated the fricative pairs.
2.3 Analyses
The similarity matrices obtained from each of the listeners were
typically not symmetrical as in the example above. Thus, the square
matix option was used in the MDS analysis (pro-ALSCAL program,
SAS Windows version 6). Since more than one similarity matrix
was involved, weighted MDS (WMDS) analysis was carried out. This
technique not only calculates the relative locations of the objects
in a space, but also calculates the relative weights that each
subject places on a particular dimension in order to find an optimal
orientation of the space. Results of 3-way, square matrix, interval
level analysis2 are presented below.
| a. Natural set
|
b. LPC22 set
|
| c. LPC10 set
|
d. LPC4 set
|
Figure 2. The stimulus configurations from 3-way interval level MDS analyses.
2.4 Results
The badness-of-fit curve and the interpretability of spatial arrangements
suggest that a 2-dimensional solution is most appropriate to model
the data. Subject spaces in WMDS showed that subjects behaved
consistently with no obvious outliers. As a further indication
of stability of the stimulus configurations, stimulus spaces from
two split-halves of subject data were also compared. The results
showed that the MDS solution of one-half of the sample is similar
to that of the other half, which means that the solution as whole
is reliable (Fox et al., 1995). This perceptual space is
presented in Figures 2a-d.
For the natural set, dimension 1 clearly separates the sibilants
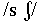 , from
nonsibilants,
, from
nonsibilants, 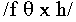 , while dimension 2 places the fricatives according to
their place of constriction, except for the fricatives /x/
and /h/. In any case, these two
fricatives are placed extremely close to each other. For the other
sets, while the 'sibilance' dimension was maintained throughout,
the ordering of fricatives on dimension 2 is not strictly according
to 'place'. Simple correlation analyses between the natural set
and the other sets with respect to the co-ordinates for the place
dimension steadily decreased from LPC22 to LPC4, thus supporting
the spatial interpretations. However, canonical correlation analyses
for the stimulus spaces for adjacent sets show that, in fact,
the spatial configurations as a whole are subject to only a very
slight change between one stimulus set and another. The coefficients
range from 1 to 0.937, and these were all significant.
, while dimension 2 places the fricatives according to
their place of constriction, except for the fricatives /x/
and /h/. In any case, these two
fricatives are placed extremely close to each other. For the other
sets, while the 'sibilance' dimension was maintained throughout,
the ordering of fricatives on dimension 2 is not strictly according
to 'place'. Simple correlation analyses between the natural set
and the other sets with respect to the co-ordinates for the place
dimension steadily decreased from LPC22 to LPC4, thus supporting
the spatial interpretations. However, canonical correlation analyses
for the stimulus spaces for adjacent sets show that, in fact,
the spatial configurations as a whole are subject to only a very
slight change between one stimulus set and another. The coefficients
range from 1 to 0.937, and these were all significant.
According to the initial hypothesis in §1, the perceptual map of natural set, which had clear phonetic interpretability, would show a poorer correlation with the corresponding auditory configuration, than the other sets. This issue is investigated in the next section.
3. Auditory spaces
In this section, we will implement various auditory distance metrics
in an attempt to account for the perceptual results obtained in
the last section. One of the principal objectives in this study
is to test how well each auditory metric predicts the perceptual
similarity of the fricatives or fricative-like sounds, and how
the predictive power of each metric varies according to the degree
of naturalness in the stimuli.
3.1 Metrics
The auditory spaces are obtained in four main stages. Firstly,
the spectra were processed by a simple 1/3-octave bandpass filtering
to model filter bank analyses in the auditory periphery. The intensity
axis is also transformed into a logarithmic scale, to reflect
the non-linear loudness density pattern in the auditory periphery.
The outcome is an auditory excitation pattern. 32-channel filters
are used for the Euclidean metric analysis, while 64-channel filters
are used for the slope and N2D metrics.
Next, spectral distances between these auditory excitation patterns are calculated with three different metrics - Euclidean, slope, and N2D metrics. The Euclidean metric takes the square root of the squared differences in the outputs of each filter between any two compared spectra. Thus, the acoustic vowel distance between two spectra S1 and S2, can be expressed as:
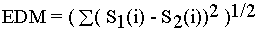
This means that the Euclidean metric gives equal weight to peaks and troughs although spectral peaks are known to have more perceptual weight than troughs. For a comparison of two excitation patterns which have the same peak locations but varying slopes of shoulders around the peaks, the Euclidean metric has been considered to be unsuitable (Klatt, 1982). As the difference between the slopes increases, the distance calculated from Euclidean metric would increase, whereas the perceptual distance would remain unchanged. This was the result of the perceptual analysis by Klatt (1982), who suggested the slope metric which emphasises the formant frequency values but is insensitive to relative formant amplitudes, or to spectral tilt changes. This effect is achieved by taking the square root of the squared differences of the first differential in the outputs of each filter.
The slope distance between two spectra, S1 and S2, with N channel filters is given by
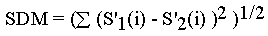
where S'1 and S'2 are the spectral slopes given by the first difference:
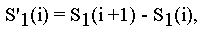 for channel number, i = 1, ..., N-1
for channel number, i = 1, ..., N-1
The negative second differential metric (N2D) of Assmann & Summerfield (1989) takes this idea further by comparing only the absolute value of the negative portions in the output spectra. In this case, spectral properties other than the formants are set to zero. Thus,
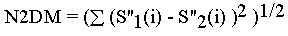
Where
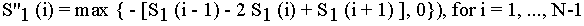
So far, the distance analyses compare a particular spectral section of each auditory excitation pattern. However this may not be accurate since articulation of fricatives also change in time. To account for the dynamic fluctuation of the fricative signal, and differences in the length between the different fricatives and speakers, a non-linear time alignment technique was used (Sakoe & Chiba, 1978). This technique is based on a simple principle of optimisation; it relies on finding the shortest path between two compared segments aligned on a graph (for illustration, see Holmes, 1988).
Now, the spectral distances are ready for the final stage of transfer into spatial configurations by the same multidimensional scaling technique used for the perceptual data. The object of this technique is to obtain an optimal spatial representation of the scaled objects on the basis of analysed distances. In this way, we determine the minimal number of dimensions required to model the data with maximal variance in the data accounted for.
3.2 Results and discussion
and 2-dimensional MDS solutions were tried out; 3-dimensional
analyses for the data were not always permitted by Proc ALSCAL.
The values for badness-of-fit were around 0.2 for the 1-dimensional
solutions, but the 1-dimensional plots were not interpretable.
2-dimensional solutions provided almost perfect fit (badness-of-fit
was almost 0) for the distance matrices. Canonical coefficients
between perceptual and auditory spaces are first reported as an
indication of the perceptual/auditory relationship.
metric |
|
| ||
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
Table2. The canonical correlation values for each of the dimensions between the perceptual and physical data, compared for different distance metrics and stimulus sets.
It is clear from the above table that only the Euclidean metric gives high and consistent correlation values. This is contrary to the expectations that the slope and N2D metrics would give more accurate predictions of the perceptual data. This result may be attributed to the specific materials used in designing these metrics in the previous studies (Klatt, 1982; Assmann & Summerfield, 1989). Indeed, Klatt's (1982) study used 66 variations of the vowel /a/ each differing subtly in terms of acoustic properties. Klatt found that pairs of synthesised /a/ vowels which differed in terms of their formant frequencies were given the highest distance scores on a '10-point scale' of 'phonetic distance' judgements (as opposed to the 'psychoacoustic distance'). This means that he needed to devise a distance metric which would emphasize the formant frequencies, whilst ignoring other spectral variations. However, when the data involve different vowels with clearly different formant positions in the spectra, it is possible that the metric may be over-emphasising the differences. Therefore, the metric may be rather specific to the particular stimulus type used. Also in the Assmann & Summerfield study (1989), there was concern over how well the pattern-matching procedure based on different distance metrics predicted the vowel identifications in the presence of competing voice (simultaneous double vowels). This means that they may have also needed to give extra emphasis to the spectral peaks, in order to allow each vowel to stand out from the other in the double vowels. Furthermore, the outputs of the slope and N2D metrics have not been transformed to MDS dimensions in previous studies. Thus, the results cannot be fully compared.
Thus, only the graphic representations of Euclidean auditory spaces are presented in Figures 3a-d. The Euclidean space has been scaled and rotated to give optimal correlation to the corresponding perceptual configuration.
| a. Natural set
|
b. LPC22 set
|
| c. LPC10 set
|
d. LPC4 set
|
Figure 3. Perceptual and auditory spaces are plotted on the same axes for comparison. (Note, that /h/ is the same point in a.)
Overall, it is remarkable how closely related the auditory organisation of 'natural' fricatives is to their perceptual organisation. As it stands, this result implies that the relationship between auditory and perceptual spaces is the same for fricatives as for the vowel cases. However, the place dimension is not clear on the auditory space. For vowels, the F1/F2 space was closely related to the traditional phonetic vowel quadrilateral, which is loosely based on articulation. However, since the auditory space here was based on the production of a particular speaker, the evidence is inconclusive. This suggests that a general auditory map of fricatives based on multiple speaker productions needs to be investigated (see the following section (§4)).
For the sets LPC22, LPC10, and LPC4, the matching between the perceptual and auditory configurations is rather impressive throughout, irrespective of whether or not a particular perceptual map was related to phonetic properties.
This rather conflicts with the hypothesis that the correlations between the perceptual and auditory maps will be higher for the stimulus sets of which the perceptual dimensions were not correlated with phonetic properties, thus reflecting the relatively direct perceptual processing involved in noise-like sounds.
In view of these unexpected results, it would be prudent to examine general physical characteristics of fricatives based on multiple speaker productions. It may be the case that either the materials used in the perception tests were atypical of English fricatives, or the general auditory space of fricatives may display dimensions which clearly correlate with phonetic properties.
4. Production tests
4.1 Materials: recordings and speakers
Five male native speakers of English in the 20-40 age group recorded
the fricatives, 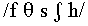 , followed by the vowel
, followed by the vowel 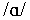 . They were asked to utter the syllables twice, clearly and in a
falling tone. The recordings were made in an anechoic room onto
a Sony DTC-1000ES digital audio tape recorder. They were digitised
as before.
. They were asked to utter the syllables twice, clearly and in a
falling tone. The recordings were made in an anechoic room onto
a Sony DTC-1000ES digital audio tape recorder. They were digitised
as before.
4.2 General auditory map of the fricatives
The results of MDS analyses for each speaker show that 2-dimensional
solutions adequately account for the data. The variance accounted
for, averaged over 10 productions, was .958 and .035 for dimensions
1 and 2 respectively. The resulting auditory spaces of each production
of each speaker were rotated for optimal congruence, and the new
sets of co-ordinates are plotted on the same axes as shown in
Figure 4.
This general auditory map of fricatives shows that all the fricative
regions are distinguished from one another, and are clearly organised
in terms of their 'place' and 'sibilance' properties. There is
an overlapping space between the fricative regions of /f/
and 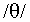 , which
is, to some extent expected, given the proximity of their perceptual
and phonetic properties. In comparison, /f/
and
, which
is, to some extent expected, given the proximity of their perceptual
and phonetic properties. In comparison, /f/
and 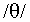 in the
Euclidean auditory space of the natural stimuli (in Figure 3a)
were much more distinct from each other, and the 'place' property
was not clear. If we consider the point corresponding to the centre
of gravity of each fricative region as its auditory prototype,
the stimuli in the perception tests may be regarded as acceptable
variants of each prototype. Thus, they could be correctly identified,
though this general auditory organisation of fricatives would
not have been found from that particular set of tokens.
in the
Euclidean auditory space of the natural stimuli (in Figure 3a)
were much more distinct from each other, and the 'place' property
was not clear. If we consider the point corresponding to the centre
of gravity of each fricative region as its auditory prototype,
the stimuli in the perception tests may be regarded as acceptable
variants of each prototype. Thus, they could be correctly identified,
though this general auditory organisation of fricatives would
not have been found from that particular set of tokens.
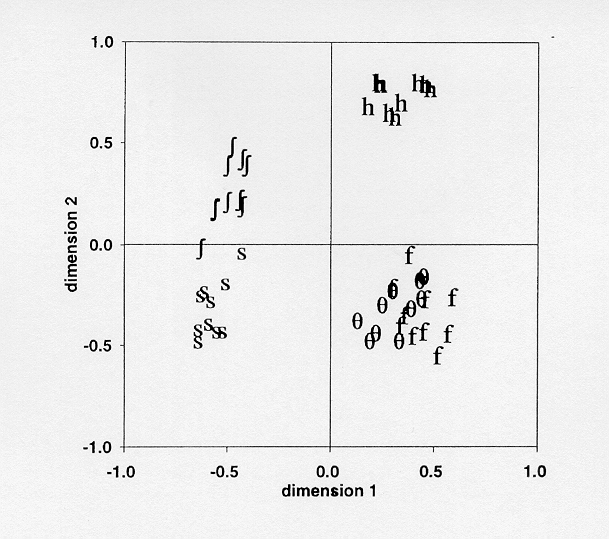
Figure 4. General auditory map of English fricatives based on 10 productions by 5 speakers.
4.3 Acoustic correlates
Although the auditory dimensions were interpreted in terms of
phonetic properties, the question of whether they may be related
to any concrete physical properties of spectra was not investigated.
In particular, there may be many acoustic parameters that correspond
to each auditory dimension, or there may be a one-to-one correspondence
between auditory and acoustic properties as in vowels. For this
purpose, the average spectral shape of each fricative type used
in the last section is placed in the corresponding region of the
fricative on the general auditory map in Figure 4. This is shown
in Figure 5.
The average spectral shape was obtained in three separate stages. First, the output energy levels of each auditory filter were averaged across the whole length of each fricative segment. In this way, for every individual production, a series of 32 numbers was obtained, representing 32 filter bands. In order to accommodate the differences in the overall level of the fricative segments, the output levels of the 32 bands were reduced by the mean level of that particular production. This process was repeated for each production of each fricative. These spectra were averaged over the ten productions spoken by the five different speakers. The horizontal axis represents the centre frequencies of the 32 filters in Hz (from 100 to 9000 Hz). The vertical axis represents the energy levels of each filter in dB (-15 to 25).
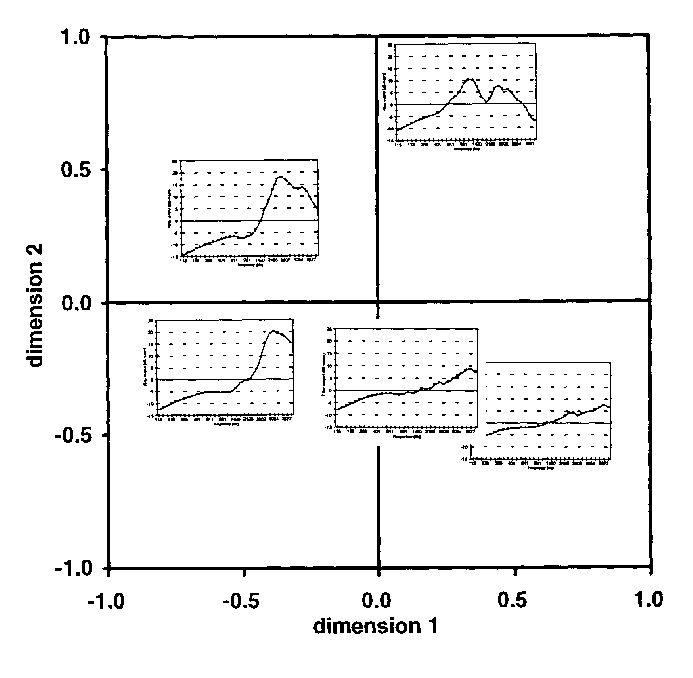
Figure 5. The average spectrum of each fricative is placed on the corresponding region of each fricative on the auditory axes in Figure 4.
It is noticeable that the spectral characteristics of /f/ and
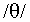 are very
similar; in both cases, the spectra are mainly flat. /s/ and
are very
similar; in both cases, the spectra are mainly flat. /s/ and 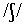 can be characterised by a single broad-band peak; however, the
low cut-off frequency occurs a little higher for /s/ at around
3600 Hz, than
can be characterised by a single broad-band peak; however, the
low cut-off frequency occurs a little higher for /s/ at around
3600 Hz, than 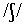 ,
at 2000 Hz. For /h/, the spectral peaks occur at around 770 Hz
and 2000 Hz, which correspond to the formant frequencies of the
following
,
at 2000 Hz. For /h/, the spectral peaks occur at around 770 Hz
and 2000 Hz, which correspond to the formant frequencies of the
following 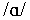 , vowel.
, vowel.
Overall, the auditory dimension 1, in Figure 5, may be related to the 'peakiness' of spectra - the maximum distance to mean amplitude - while dimension 2 may be related to the centre of gravity of the spectra.
5. Conclusion
The principal achievement of this research is that studies of
spatial representations on vowels have been successfully replicated
in a set of consonants, and furthermore, that the findings are
congruent with those obtained in vowel studies. The results have
shown a close relationship between perceptual and auditory spaces;
and the phonetic and physical correlates of these spaces have
also been identified. Therefore, the study of spatial representations
enables us to identify key factors involved in each domain of
the processing, and to demonstrate simple correlation across the
different domains. This result stands in sharp contrast to the
contemporary detailed cue studies in which many different spectral
characteristics seem to be intricately interwoven and often interact
in specifying the perception of any one fricative category.
Another important finding was that the auditory processing in the fricative data was adequately modelled by the auditory transformations used in the vowel data. A 1/3-octave bandpass filter bank analysis, coupled with non-linear intensity scaling, adequately modelled the essential peripheral perceptual processing. In order to account for the time-varying spectral properties in fricatives, a non-linear time alignment procedure was employed. Auditory distances between fricatives were most accurately modelled by the Euclidean distance metric; the resulting auditory representations were then found to be congruent with spatial representations in other domains, as well as with the spectral properties of fricatives.
A limitation within the present study was that the axes in the phonetic (place and sibilance features) and acoustic spaces were not directly measured; they were merely referenced as possible correlates to the perceptual and auditory dimensions. In particular, the actual values of 'peakiness' of spectra and frequency of the main peak (described in §4) should be measured directly in future.
The validity of the spatial approach needs to be confirmed with respect to the phenomena of normalisation, coarticulation, and with other types of consonants, for example, the plosives. It also needs to be applied to other languages, with different phonological structures, in which the occupation of the space differs and the imputed criteria for identifying a segment may change.
The relationships between phonetic, and auditory spaces were expected to vary with the quality (degree of artificiality) of stimuli and listening modes (speech vs. nonspeech). However, the differences in perception between the stimulus sets were very subtle, and the significance of any changes could only be confirmed in relation to the correlation between the perceptual and corresponding auditory maps. The initial hypothesis was that the stimuli with phonetically interpretable perceptual dimensions would be less well correlated to their corresponding auditory dimensions than other stimuli. As already alluded to, however, the correlation between the perceptual and auditory spaces were high for all the stimuli sets. This may be attributed to the fact that the general auditory space (Figure 4) was clearly related to phonetic properties; thus, both natural and very artificial stimuli are expected to show high correlation between spaces. It seems that the perception of both speech and nonspeech sounds is well accounted for by their auditory properties. The difference between speech and nonspeech perception processes lies in the fact that, for speech sounds, auditory organisation is clearly related to phonetic properties.
Overall, these results suggest a unified experimental paradigm in which the development of speech perception models may be investigated in parallel for both vowels and consonant in terms of spatial representations.
Acknowledgements
Many thanks to Stuart Rosen and other members of Wolfson House
for their help and advice.
References
Assmann, P. F. & Summerfield, Q. (1989) Modelling the perception
of concurrent vowels: Vowels with the same fundamental frequency.
Journal of the Acoustical Society of America 85. 327-338.
Choo, W. (1996) Relationships between phonetic perceptual and auditory spaces for fricatives. PhD thesis. University of London.
Fox, R. A., Fledge, J. E. & Munro, M. J. (1995) The perception of English and Spanish vowels by native English and Spanish listeners: A multidimensional scaling analysis. Journal of the Acoustical Society of America 97. 2540-2551.
Harman, H. H. (1967) Modern Factor Analysis. The University of Chicago Press, Chicago.
Holmes, J. N. (1988) Speech Synthesis and Recognition. Van Nostrand Reinhold, UK.
Klatt, D. H. (1982) Prediction of perceived phonetic distance from critical-band spectra: a first step. Proc. ICASSP-82: IEEE transaction. Acoustics, Speech, and Signal Processing . 1278-1281.
Klein, W., Plomp, R. & Pols, L. C. W. (1970) Vowel spectra, vowel spaces and vowel identification. Journal of the Acoustical Society of America 48. 999-1009.
Krull, D. (1990) Relating acoustic properties to perceptual responses: A study of Swedish voiced stops. Journal of the Acoustic Society of America 88. 2557-2570.
Kruskal, J. B. (1964) Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 29. 1-27.
Kuhl, P. K. (1995) Mechanisms of developmental change in speech and language. Proc. ICPhS 95 Stockholm. Vol. 2, 132-139.
Pols, L. C. W., van der Kamp, L. J. Th. & Plomp, R. (1969) Perceptual and physical space of vowel sounds. Journal of the Acoustical Society of America 46. 456-467.
Sakoe, H. & Chiba, S. (1978) Dynamic programming algorithm optimization for spoken word recognition. IEEE transaction. Acoustics, Speech, and Signal Processing 26. 43-49.
© Won Choo and Mark Huckvale
 for comments
for comments