UCL Department of Phonetics and Linguistics
Introduction to Computer Programming with MATLAB
Lecture 9: Spectral Analysis
Objectives
By the end of the session you should:
q know how to build and perform a filterbank analysis of a signal
q know how to use the discrete fourier transform to convert a waveform to a spectrum and vice versa.
q know how to divide a signal into overlapping windows
q know how to calculate and display a spectrogram
Outline
1. Filterbank analysis
The most flexible way to perform spectral analysis is to use a bank of bandpass filters. A filterbank can be designed to provide a spectral analysis with any degree of frequency resolution (wide or narrow), even with non-linear filter spacing and bandwidths. A disadvantage of filterbanks is that they almost always take more calculation and processing time than discrete Fourier analysis using the FFT (see below).
To use a filter bank for analysis we need one band-pass filter per channel to do the filtering, a means to perform rectification, and a low-pass filter to smooth the energies. In this example, we build a 19-channel filterbank using bandwidths that are modelled on human auditory bandwidths. We rectify and smooth the filtered energies and convert to a decibel scale.
function e=auditoryfbank(x,fs)
% AUDITORYFBANK performs an auditory filterbank analysis on a signal
% E=AUDITORYFBANK(X,FS) passes signal X, sampled at FS samples/sec
% through a 19-channel auditory filterbank, smoothing and downsampling
% energies to 100 frames per second. Output is in decibels.
%
% get output energy sample points
x=reshape(x,[length(x) 1]); % force to be a column
eidx=fs/100:fs/100:length(x); % sampling indices (100 frame/sec)
ne=length(eidx); % number of output energy frames
% these are the filter cut-offs
cuts=[180 300 420 540 660 780 900 1075 1225 1375 1525 1700 1900 2100 2300 2550 2850 3150 3475 4000];
nf=length(cuts)-1; % number of filters
% initialise the output energy table
e=zeros(ne,nf);
% build a smoothing filter
[sb,sa]=butter(4,2*50/fs); % low-pass at half output frame rate
% for each channel in turn
for i=1:nf
fprintf('Calculating channel %d (%d-%dHz)\n',i,cuts(i),cuts(i+1));
% build the band-pass filter
[b,a]=butter(4,[2*cuts(i)/fs 2*cuts(i+1)/fs]);
% filter the signal
y=filter(b,a,x);
% rectify and smooth
sy=filter(sb,sa,abs(y));
% sample and convert to decibels
sy=max(sy,eps); % force to be > 0
e(:,i)=100+20*log10(sy(eidx)); % downsample and convert to dB
end
The input to this function is a waveform, x, sampled at fs samples/second. The output is a table of energies, e, in which each row represents 10ms of the signal, and each column the energy in decibels found in a band-pass filtered frequency region at that time.
In this example, we build a chirp and pass it through the filterbank, then plot the output energies in each channel against time:
% build a chirp from 500 to 2000Hz
t=0:1/10000:1;
f=linspace(500,2000,length(t));
y=sin(2*pi*f.*t);
soundsc(y,10000);
% put through filter bank
e=auditoryfbank(y,10000);
% scale to 0..1, and transpose
emin=min(min(e));
emax=max(max(e));
te=((e-emin)/(emax-emin))'
% offset each channel by channel number for plot
for i=1:size(te,1)
te(i,:) = te(i,:)+i;
end
plot(1:size(te,2),te,'k-');
ylabel('Filter channel');
xlabel('Frame number');

2. Spectral analysis using Fourier transform
The discrete-time discrete-frequency version of the Fourier transform (DFT) converts an array of N sample amplitudes to an array of N complex harmonic amplitudes. If the sampling rate is Fs, the N input samples are 1/Fs seconds apart, and the output harmonic frequencies are Fs/N hertz apart. That is the N output amplitudes are evenly spaced at frequencies between 0 and (N-1).Fs/N hertz.
To compute the DFT in MATLAB, we use the function fft(x,n). This function takes a waveform x and the number of samples n. When n is less than the length of x, then x is truncated; when n is longer than the length of x, then x is padded with zeros. The output is an array of complex amplitudes of length n. You can obtain the magnitude of each spectral component with abs(), and its phase with angle() (result in radians).
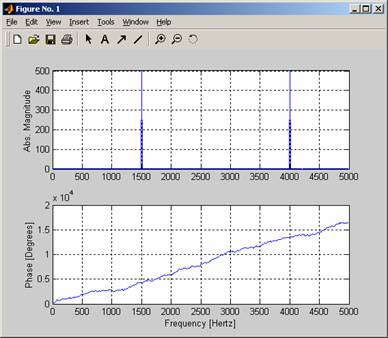
In this example, we generate a complex periodic signal, then calculate and display the magnitude spectrum and the phase spectrum:
% generate a complex signal
fs = 10000; % sampling rate
t = 0:1/fs:0.1; % sampling instants
x = sin(2*pi*1500*t) + sin(2*pi*4000*t); % two sinusoids
%
% perform 1000-point transform
y = fft(x,1000); % y contains 1000 complex amplitudes
y = y(1:500); % just look at first half
m = abs(y); % m = magnitude of sinusoids
p = unwrap(angle(y)); % p = phase of sinusoids, unwrap()
% copes with 360 degree jumps
% plot spectrum 0..fs/2
f = (0:499)*fs/1000; % calculate Hertz values
subplot(2,1,1), plot(f,m); % plot magnitudes
ylabel('Abs. Magnitude'), grid on;
subplot(2,1,2), plot(f,p*180/pi); % plot phase in degrees
ylabel('Phase [Degrees]'), grid on;
xlabel('Frequency [Hertz]');
The fft() function calculates the discrete fourier transform in the most efficient way possible, but transforms of length 2m (m=integer) are considerably fastest to calculate. Use sizes of 512, 1024, etc for the fastest speed.
Typically we want the magnitude or the power of a spectrum in decibels, which can be obtained with:
Y=fft(x,1024);
magnitude = abs(Y);
powerdB=20*log10(magnitude+eps);
To convert back from harmonic amplitudes to a waveform use the inverse discrete Fourier transform function ifft(). Be aware that this function takes complex harmonic amplitudes and delivers complex sample amplitudes. Use the function real() to get the real part of the signal amplitudes:
Y=fft(x1,1024); % waveform -> spectrum
%%% process Y in some way %%%
x2=real(ifft(Y)); % spectrum -> waveform
3. Windowing a signal
Often we want to analyse a long signal in overlapping short sections called “windows”. For example we may want to calculate an average spectrum, or to calculate a spectrogram. Unfortunately we cannot simply chop the signal into short pieces because this will cause sharp discontinuities at the edges of each section. Instead it is preferable to have smooth joins between sections. Raised cosine windows are a popular shape for the joins:
You can use the MATLAB function hamming() to design smooth windows of a given length, and then you can use code such as the following to divide the signal into sections:
% divide up a signal into windows
x = sin(2*pi*500*(1:10000)/10000); % example signal
nx = length(x); % size of signal
w = hamming(32)'; % hamming window
nw = length(w); % size of window
pos=1;
while (pos+nw <= nx) % while enough signal left
y = x(pos:pos+nw-1).*w; % make window y
%%%% process window y %%%%
pos = pos + nw/2; % next window
end
4. Spectrograms
MATLAB has a built-in function specgram() for spectrogram calculation. This function divides a long signal into windows and performs a fourier transform on each window, storing complex amplitudes in a table in which the columns represent time and the rows represent frequency.
Call the specgram function on a signal x with a call:
[B,f,t] = specgram(x,nfft,fs,window,overlap)
Here, nfft is size of the fourier transform, use this to control the number of frequency samples on the vertical axis of the spectrogram; fs is the sampling rate of the input signal; window is the number of input samples per vertical slice, use this to control the analysis bandwidth; overlap is the number of samples by which adjacent windows overlap, use this to control the number of vertical slices per second. The output B is a table of complex amplitudes; f is a vector of frequency values used to label the rows, and t is a vector of time values used to label the columns.
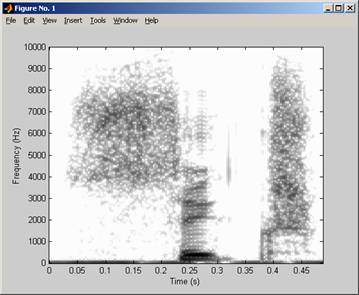
Here is a complete example, in which we also use the imagesc() and colormap() functions to display the results on a conventional grey scale representing the top 50dB of the signal:
% get a portion of signal
[y,fs]=wavread('six.wav',[2000 12000]);
%
% calculate the table of amplitudes
[B,f,t]=specgram(y,1024,fs,256,192);
%
% calculate amplitude 50dB down from maximum
bmin=max(max(abs(B)))/300;
%
% plot top 50dB as image
imagesc(t,f,20*log10(max(abs(B),bmin)/bmin));
%
% label plot
axis xy;
xlabel('Time (s)');
ylabel('Frequency (Hz)');
%
% build and use a grey scale
lgrays=zeros(100,3);
for i=1:100
lgrays(i,:) = 1-i/100;
end
colormap(lgrays);
Reading
An essential introduction to spectral analysis can be found in Rosen & Howell, Signals and Systems for Speech and Hearing, Academic Press, 1990; ISBN: 0125972318.
Units 5 and 6 from the Introduction to Digital Signal Processing course at http://www.phon.ucl.ac.uk/courses/spsci/dsp/ provides more mathematical detail about fourier analysis and windowing.
The best introduction to signal processing is the book: Introductory Digital Signal Processing with Computer Applications, by P.A. Lynn, W. Fuerst, B. Thomas, Paperback - 494 pages 2nd edition (1998) John Wiley and Sons; ISBN: 0471976318
Exercises
For these exercises, use the editor window to enter your code, and save your answers to files under your account on the central server. When you save the files, give them the file extension of ".m". Run your programs from the command window.
1. Write a program (ex91.m) that asks the user for a filename (WAV file), then loads the first 1024 samples, applies a Hamming window and calculates the power spectrum. Plot the windowed signal and the spectrum on a single figure with waveform at the top and the spectrum at the bottom. Make sure you express the spectral amplitudes in decibels.
2. Adapt the last exercise (ex92.m) to calculate and display the average spectrum for the whole file.
3. Write a program (ex93.m) that calculates a high-resolution linear filterbank analysis of a given file and displays the results on a grey scale, following spectrogram conventions. Use at least 128 overlapping band-pass filters with bandwidths of 300Hz and an output rate of 1000 frames/sec.
4. (Homework) Write a program that filters a signal in the frequency domain. That is: it takes a signal, divides it up into overlapping window segments, then for each segment calculates a FFT, modifies the spectral magnitudes according to the required frequency response, then performs an inverse FFT to make a filtered segment. The filtered segments can then be added together to create the filtered output signal.