UCL Department of Phonetics and Linguistics
Introduction to Computer Programming with MATLAB
Lecture 3: Graph Plots
Objectives
By the end of the session you should:
q be able to create data sets and display simple x-y graphs
q know the names of some basic MATLAB functions and what they do
q be able to calculate some simple waveforms
q be able to replay waveforms and also save and load them from disk
Outline
1. Basic Plotting
To create XY graphs, it is easiest to form your data into two row vectors, one for the x co-ordinates, and one for the y co-ordinates. The command
plot(x,y)
will then create a figure with points at each y value for each matching x value. You can control the style of any line drawn through the points by a third string argument to the plot command:
plot(x,y,style);
where style is made up from characters as follows:
q Color strings are 'c', 'm', 'y', 'r', 'g', 'b', 'w', and 'k'. These correspond to cyan, magenta, yellow, red, green, blue, white, and black.
q Linestyle strings are '-' for solid, '--' for dashed, ':' for dotted, '-.' for dash-dot, and none for no line.
q The marker types are '+', 'o', '*', and 'x' and the filled marker types 's' for square, 'd' for diamond, '^' for up triangle, 'v' for down triangle, '>' for right triangle, '<' for left triangle, 'p' for pentagram, 'h' for hexagram, and none for no marker.
For example:
x = [ 1 2 3 4 ];
y = [ 10 15 20 25 ];
plot(x,y,g-*);
You can plot multiple lines by repeating the arguments:
plot(x1,y1,x2,y2, );
or
plot(x1,y1,style1,x2,y2,style2, );
You can give the graph a title with the
title(label);
command, where label is a character string. Likewise you can add labels to the X and Y axes with
xlabel(label);
and
ylabel(label);
You can add a legend with
legend(label1,label2,label3, );
2. Built in functions
Generation
|
zeros() |
matrix of specified size filled with zeros |
|
ones() |
matrix of specified size filled with ones |
|
rand() |
generate pseudo random number(s) between 0 and 1 |
Arithmetic
|
rem() |
remainder after integer division |
|
abs() |
absolute value (also character -> number) |
|
fix() |
truncate a value to its integer part (towards zero) |
|
round() |
round a value to nearest integer. |
|
sqrt() |
square root |
|
sin() |
sine (angle in radians) |
|
cos() |
cosine (angle in radians) |
|
exp() |
exponential |
|
log() |
natural logarithm |
|
log10() |
logarithm base 10 |
Status
|
length() |
length of a vector (longest dimension of matrix) |
|
size() |
size of a matrix [nrows, ncols] |
Miscellaneous
|
sum() |
sum the elements of a vector |
|
mean() |
find mean of elements of a vector |
|
sort() |
sort the elements of a vector in increasing size |
|
clock() |
returns date and time as a vector [year month day hour minute seconds] |
|
date() |
returns date as a string dd-mmm-yyyy |
3. Generating Waveforms
Waveforms are just long vectors with one number per amplitude sample. Usually they are best kept scaled so that each amplitude is between 1 and 1. To generate a sinewave, first generate a time sequence t representing the times of each sampling instant; for example:
t = 0:0.0001:2;
would generate a two second sequence with a sampling interval of 0.1ms (i.e. 10,000Hz). You can then generate a sinewave at frequency F with the expression
y = sin(2*pi*F*t);
You can create a pulse by creating a vector of zeros and setting a single element to one. A pulse train has a series of elements set to one. If these occurred every 100 elements, you might use the expression
y(1:100:10000)=1;
To create a simple sawtooth, you can use the remainder function, for example
y = rem(1:10000,100)/100;
To create a noise waveform, you can use the rand(nrows,ncols) function, for example
y = rand(1,10000);
4. Sound Replay, Load and Save
To replay a waveform, you can use
sound(wave,samplerate);
To ensure that the waveform is scaled to the range 1 .. +1 before replay, use
soundsc(wave,samplerate);
instead.
To save a waveform to a file, use
save filename variable;
To load a waveform from a file, use
load filename variable;
To save a waveform in a Windows compatible audio file format, use
wavwrite(waveform,samplerate,filename);
To load a Windows compatible audio file, use
[waveform,samplerate,nbits]=wavread(filename);
Reading
"Getting Started: Graphics" in MATLAB Help.
Exercises
For these exercises, use the editor window to enter your code, and save your answers to files under your account on the central server. To run the programs, use the Debug/Run menu option or cut and paste the code into the command window. When you save the files, give them the file extension of ".m".
1. Draw a graph that joins the points (0,1), (4,3), (2,0) and (5,-2). (ex31.m).
2. Draw a target made up of three circular rings of radius 1, 2 and 3 (ex32.m). The formula for the co-ordinates of a circle are:
|
x = r.cos(θ) |
0 < θ < 2π |
|
y = r.sin(θ) |
r > 0 |
You may need to use the command axis('equal'), why?
3. The seeds on a sunflower are distributed according to the formula below. Plot a small circle at each of the first 1000 co-ordinates (ex33.m):
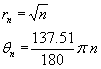
4. Calculate 10 approximate points from the function y=2x by using the formulae:
xn = n
yn = 2n + rand - 0.5
Fit a line of best fit to these points using the function polyfit() with degree=1, and generate co-ordinates from the line of best fit using polyval(). Use the on-line help to find out how to use these functions. Plot the raw data and the line of best fit. (ex34.m).
5. Calculate and replay 1 second of a sinewave at 500Hz with a sampling rate of 11025Hz. Save the sound to a file called "ex35.wav". Plot the first 100 samples (ex35.m).
6. (Advanced) Calculate and replay a 2 second chirp. That is, a sinusoid that steadily increases in frequency with time, from say 250Hz at the start to 1000Hz at the end. (ex36.m).
7. (Homework) Build a square wave by adding together 10 odd harmonics: 1f, 3f, 5f, etc. The amplitude of the nth harmonic should be 1/n. Display a graph of one cycle of the result superimposed on the individual harmonics.