UNIT 6:

WINDOWING

Summary

This unit considers the consequences of analysing sections or 'windows' of a continuous signal, and how the use of smoothing functions reduces the spectral artifacts introduced.

When you have worked through this unit you should:

· be able to state why and when spectral leakage occurs

· understand how a smooth window reduces the amount of spectral leakage

· be able to describe and apply a Hamming window in your own work

Concepts

Where the frequency components of signals we analyse with the DFT are exact harmonics of the DFT analysis, the resulting spectrum shows clean spectral lines. Since mostly the signals we want to analyse will not contain just these harmonics, we find that the energy at one input frequency is spread to a number of nearby harmonics in the DFT. This is called spectral leakage.

A similar problem arises for signals which are changing with time, where we usually want to analyse a 'snapshot' of the signal, short enough in which we could consider the generating system to be 'stationary'. To do this we must take a sample or a window of the signal over some defined interval. If we simply cut out a section of the signal, however, we introduce artifacts into the waveform - namely the sudden onset and offset - which will be manifested as distortions in our spectral analysis. What is happening is that our spectrum results from the convolution of the signal spectrum with the spectrum of a rectangular window. The spectrum of a rectangular window has the familiar sin(x)/x shape or sinc function, and so each signal component is broadened by this shape.

We can reduce these distortions by ensuring that the section has no sudden onset or offset, which we can do by multiplying our section with a smoothing function which reduces the size of the signal at the edges. We need a shape which has a spectrum with a narrow central lobe and small sidelobes. A window based on a raised-cosine shape called the Hamming window is a common compromise:

1

Where N is the number of samples in the section. See Hamming().

Algorithms

// window.cpp -- Hamming window functions

//

// C++ (c) 1996 Mark Huckvale University College London

#include "tools.h"

#include "window.h"

// apply hamming window to a waveform

Waveform Hamming(const Waveform& iwv)

{

Waveform owv(iwv.count(),iwv.rate());

double omega = 2.0 * PI / (iwv.count()-1);

for (int i=1;i<=owv.count();i++)

owv[i] = (0.54 - 0.46 * cos(omega*(i-1))) * iwv[i];

return owv;

}

// apply hamming window to a complex waveform

ComplexWaveform Hamming(const ComplexWaveform& iwv)

{

ComplexWaveform owv(iwv.count(),iwv.rate());

double omega = 2.0 * PI / (iwv.count()-1);

for (int i=1;i<=owv.count();i++)

owv[i] = (0.54 - 0.46 * cos(omega*(i-1))) * iwv[i];

return owv;

}

Bibliography

Lynne & Fuerst Introductory Digital Signal Processing, Section 8.2.2

Example Program 6.1

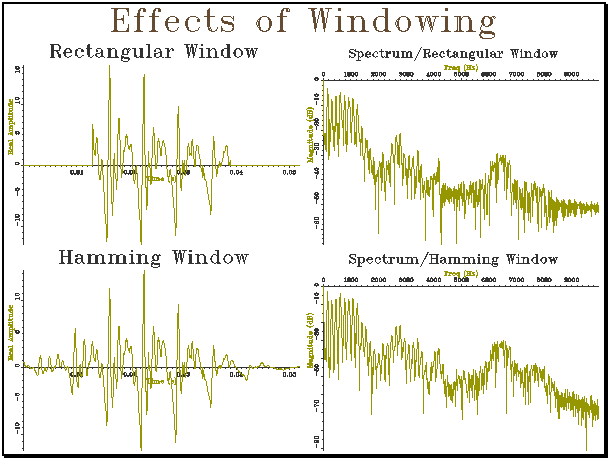
// window_t.cpp -- demonstration of windowing

#include "tools.h"

#include "quantise.h"

#include "cfft.h"

#include "window.h"

#include "annot.h"

const char *FILENAME="/users/mark/trial”;

const char *SPITEMNO="sp";

const char *ANITEMNO="an";

const char *ANLABEL="V";

// load waveform sample from test signal

ComplexWaveform ReadSample()

{

// read in annotation

AnnotationList anlist;

if (anlist.load(FILENAME,ANITEMNO)!=0) {

cerr << "Could not find annotations\n";

exit(0);

}

// find annotation

Annotation an = anlist.find(ANLABEL);

if (!an.name) {

cerr << "Could not find annotation\n";

exit(0);

}

// load appropriate section

Signal isig(1,1.0);

isig.load(FILENAME,SPITEMNO,an.posn,an.size);

// convert to waveform then complex

Waveform iwv = MakeCont(isig,0.001);

ComplexWaveform cwv = WaveformToComplexWaveform(iwv);

return cwv;

}

int main()

{

// set up graphs

Graph gr(2,2,"Effects of Windowing");

// load sample waveform

ComplexWaveform wv1 = ReadSample();

// apply rectangular window and plot

for (int i=1;i<=wv1.count()/4;i++) wv1[i]=0.0;

for (int i=(3*wv1.count())/4;i<=wv1.count();i++) wv1[i]=0.0;

wv1.plotReal(gr,1,"Rectangular Window");

// FFT without windowing and plot

Spectrum sp1 = ComplexFFT(wv1);

(sp1.half()).plotLogMag(gr,2,"Spectrum/Rectangular Window");

// apply Hamming window and plot

ComplexWaveform wv2 = Hamming(ReadSample());

wv2.plotReal(gr,3,"Hamming Window");

// FFT with Hamming window and plot

Spectrum sp2 = ComplexFFT(wv2);

(sp2.half()).plotLogMag(gr,4,"Spectrum/Hamming Window");

gr.close();

}

Exercise

6.1 Adapt Example 6.1 to plot the waveforms and FFT spectra of sine waves at F_s/4 (exact) and F_s/6 (non-exact) harmonic frequencies with rectangular and Hamming windows. Use a short FFT of about 128 samples. Interpret the results.