UNIT 7:

DIGITAL FILTER

DESIGN

Summary

This unit is concerned primarily with the design of digital systems having frequency response characteristics appropriate to low-pass, high-pass and band-pass filters. It is concerned with both non-recursive and recursive designs: the former based on the Fourier transform method, the second through the so-called ‘bilinear’ transformation of analogue designs.

When you have worked through this unit you should:

· be able to explain how simple non-recursive filters may be designed by the DFT method

· understand how low-pass non-recursive filters may be transformed into high-pass and band-pass designs

· understand how the Kaiser window provides a means for building a simple non-recursive filter from specifications of the stop-band ripple and the width of the transition region.

· be able to explain how simple recursive filters may be designed through the use of the Butterworth formulae

· understand how the use of cascaded second-order sections provides a means for implementing Butterworth filters from the pole-zero diagram

· understand how recursive low-pass filters may be transformed into high-pass and band-pass designs.

· be able to discuss the relative merits of recursive and non-recursive designs for different applications.

Concepts

Non-recursive Filter Design

We seek to find a set of a[] (numerator) coefficients for a linear time-invariant system that would implement a low-pass filter: that is the impulse response of a low-pass non-recursive filter. We then consider how to transform these coefficients into high-pass or band-pass forms.

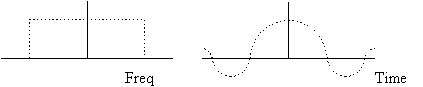
We first note that the Fourier transform of a rectangular window has a characteristic shape known as a sin(x)/x or sinc(x) function. Thus for an ideal low-pass filter response, which has a rectangular shape, the related impulse response must follow this sin(x)/x shape. Since the response of a digital system repeats periodically with frequency (once per sampling frequency), we can choose to consider a rectangular filter within a response that extends from -sample-rate/2 to +sample-rate/2, and this will give us an impulse response that is also symmetric about t=0:

For a cut-off angular frequency of w_c the formula for this impulse response is just:

where w_c = 2pf_c, where f_c = fraction of sampling rate, and where n extends over all positive and negative times.

To generate an impulse response of a certain maximum size, it is best to window the resulting coefficients, rather than simply truncate them. This can be easily performed with a Hamming window. We may then shift the filter coefficients in time to get a causal filter. See NRLowPass().

To obtain the impulse response of a high-pass or band-pass filter, we note that all we need do is shift the frequency response curve along the frequency axis - so the rectangular response is now either symmetric about the half-sample-rate frequency - in which case we get a high-pass filter, or is now over a block of frequencies - in which case we get a band-pass filter. The process of shifting the response in the frequency domain is a process of convolution with another response which consists solely of an impulse at the new centre frequency of the block, that is the spectrum of a signal having a single frequency component at the new centre frequency, that is the spectrum of a sinusoidal signal. This convolution in the frequency domain manifests itself in the time domain by a multiplication of the impulse response by a cosine wave of the appropriate frequency. So to shift the impulse response of a low-pass filter up to a new centre angular frequency w, we generate:

For the special case that the new rate is half the sample rate (i.e. when w=p) the modulation consists of multiplying h[] by +1, -1, +1, -1, .... See the implementations of NRHighPass() and NRBandPass() to exemplify this.

While the Hamming window is a simple and useful method for truncating the impulse response, it is rather inflexible. The Hamming window gives us a flat pass band and fairly good attenuation in the stop band, but at the expense of a fairly broad transition band. Sometimes we wouldn't mind more ripple in the pass band if that allowed us to have a narrower transition region. We can achieve this by designing a windowing function with the appropriate properties and use that to truncate the sinc function impulse response. A simple way to achieve this is with the parametric Kaiser window.

The Kaiser window is defined as:

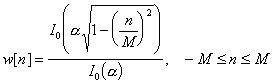
Where I₀ is the zeroth order modified Bessel function of the first kind, which has a complex mathematical description, but a straightforward algorithmic description shown in Algorithm 7.2. The parameter a controls the tradeoff between transition width and ripple. We can give a heuristic for the selection of a and M from a specification of (i) the allowed stop band ripple A expressed as decibels below the passband, and (ii) the transition width D expressed as a fraction of the sample rate:

if A >= 50, then a = 0.1102(A - 8.7)

if 21 < A < 50, then a = 0.5842(A - 21)^0.4 + 0.07886(A - 21)

if A <= 21, then a = 0

Where the ripple level is less than 21dB from the pass band, then we end up with a rectangular window. M, the half-size of the window is then given by:

Algorithm 7.2, Kaiser designs a window according to these formulae, which could be used to substitute for the Hamming window used in NRLowPass, etc.

Recursive Filter Design

The design of recursive filters is considerably more complex than the design of non-recursive filters. The design task is to place poles and zeros on the complex plane, such that the frequency response has the desired characteristics. This can either be performed through experience or with an interactive design tool. We choose to look at the design formulae developed for analogue filters: specifically for Butterworth designs. These can then be transformed into the digital domain through the use of an algebraic transformation that maps the analogue frequencies 0..¥ into the periodically repeating angular frequencies 0..2p. The mechanism used is called the bilinear transformation.

A digital Butterworth low-pass filter of order n has n poles arranged on a circular arc on the complex plane and n zeros located at z = (-1,0). If n is even, the poles form n/2 conjugate pairs. If n is odd, then a pole on the real axis is added. If we keep to even n for convenience the location of the poles are given by the formulae:

where the real and imaginary parts are given by:

and where

For simplicity of implementation, the routine ButterworthPoles() calculates the positions of n/2 poles on the positive imaginary axis, and each pole-pair is then used to implement a separate linear system (a second-order section) in the routine ButterworthLowPass(). The resulting chain of linear systems is returned for filtering operation.

The transformation of the low-pass design into high-pass is straightforward: it simply involves reflecting the poles and zeros around the imaginary axis. See ButterworthHighPass().

The transformation of the low-pass design into band-pass is more complex and involves a doubling of the filter order and a rotation of the poles around the unit circle. For a band-pass filter extending from angular frequencies w_l to w_h, we first calculate the poles and zeros for a low pass filter with a cut-off frequency w_c = (w_h‑w_l)/2. Then each pole or zero at z is moved to a new location by the formula:

where A is given by:

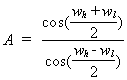
See ButterworthBandPass().

A Butterworth design gives us a filter with a maximally-flat passband and good stop-band attenuation, so that it makes a good general purpose filter. As before, however, other designs can give us a narrower transition region at the cost of greater ripples in the pass- and/or stop-bands. Many DSP packages give design programs for Chebyshev and Elliptic filter designs, but their essential operation is the same as the Butterworth design.

Algorithms

Algorithm 7.1 Non-recursive filter design

// nonrec.cpp -- non-recursive filter design

// NRLowPass() build NR low-pass filter

// NRHighPass() build NR high-pass filter

// NRBandPass() build NR band-pass filter

#include "tools.h"

#include "ltisys.h"

// sinc() or sin(x)/x function

double sinc(double x)

{

if (x==0)

return cos(x);

else

return sin(x)/x;

}

// Create non-recursive low-pass filter by Fourier Transform method

LTISystem NRLowPass(

double freq, // corner freq (fraction of sampling rate)

int ncoeff // # coefficients

) // returns LTI system to specification

{

int i;

// convert frequency

double omega = 2 * PI * freq;

// build half-sized window from sinc function

int nhalf = ncoeff/2;

Waveform hwv(nhalf,1.0);

for (i=1;i<=nhalf;i++)

hwv[i] = omega * sinc(i*omega)/PI;

// window with (half-)hamming window

for (i=1;i<=nhalf;i++)

hwv[i] *= 0.54 + 0.46 * cos(i*PI/nhalf);

// create new LTI System

LTISystem lpfilt(2*nhalf,0);

// copy impulse response into system

// (indexed -nhalf .. 0 .. nhalf)

lpfilt.a[nhalf] = omega/PI;

for (i=1;i<=nhalf;i++) {

lpfilt.a[nhalf-i] = hwv[i];

lpfilt.a[nhalf+i] = hwv[i];

}

return lpfilt;

}

// create high-pass non-recursive filter from low-pass prototype

LTISystem NRHighPass(

double freq, // corner freq (fraction of sampling rate)

int ncoeff // # coefficients

) // returns LTI system

{

// get low-pass version

LTISystem hpfilt = NRLowPass(0.5-freq,ncoeff);

// now modulate with cos(n*PI) = +1,-1,+1,-1,...

int nhalf = hpfilt.a.count()/2;

for (int i=1;i<=nhalf;i+=2) {

hpfilt.a[nhalf-i] = -hpfilt.a[nhalf-i];

hpfilt.a[nhalf+i] = -hpfilt.a[nhalf+i];

}

return hpfilt;

}

// create band-pass non-recursive filter from low-pass prototype

LTISystem NRBandPass(

double lofreq, // low corner freq (fraction of sampling rate)

double hifreq, // high corner freq (fraction of sampling rate) }

int ncoeff // # coefficients

) // returns LTI system

{

// get low-pass prototype

LTISystem bpfilt = NRLowPass((hifreq-lofreq)/2,ncoeff);

// now modulate with cos(n*centrefreq)

int nhalf = bpfilt.a.count()/2;

double cf = 2*PI*(lofreq+hifreq)/2;

bpfilt.a[nhalf] = 2 * bpfilt.a[nhalf];

for (int i=1;i<=nhalf;i++) {

bpfilt.a[nhalf-i] = 2 * bpfilt.a[nhalf-i] * cos(i*cf);

bpfilt.a[nhalf+i] = 2 * bpfilt.a[nhalf+i] * cos(i*cf);

}

return bpfilt;

}

Algorithm 7.2 - Kaiser Window

// kaiser.cpp - Kaiser window design

#include "tools.h"

#include “kaiser.h”

// zeroth order modified Bessel function of the first kind

const int ITERLIMIT=15;

const double CONVERGE=1.0E-8;

double besselI0(double p)

{

// initialise iterative loop

p = p/2;

double n = 1, t = 1, d = 1;

// iteration

int k = 1;

double v;

do {

n = n * p; d = d * k;

v = n / d; t = t + v * v;

} while ((++k < ITERLIMIT) && (v > CONVERGE));

return t;

}

// return half-Kaiser window to specification

Waveform Kaiser(

double ripple, // input stop-band ripple (dB)

double twidth, // input transition width

// (fraction of sample rate)

int kmaxlen) // maximum window size

{

double alpha; // window coefficient

int hlen; // half window length

// set Kaiser window coefficient (design rule)

if (ripple <= 21)

alpha = 0;

else if (ripple < 50)

alpha = 0.5842*exp(0.4*log(ripple-21))+0.07886*(ripple-21);

else

alpha = 0.1102*(ripple - 8.7);

// set Kaiser window size (design rule)

if (ripple < 7.95)

hlen = 0;

else

hlen = 1+(int)((ripple - 7.95)/(28.72*twidth));

if ((hlen+1) > kmaxlen) hlen = kmaxlen - 1;

// build window

Waveform kwin(hlen+1,1.0); // output window

// calculate window 1..hlen+1

double d = besselI0(alpha);

kwin[1] = 1.0;

for (int n=1;n<=hlen;n++) {

double v = n/(double)hlen;

kwin[n+1] = besselI0(alpha*sqrt(1-v*v))/d;

}

return kwin;

}

Algorithm 7.3 Butterworth Recursive Filter Design

// ltisysch.h -- LTI System Chain class declaration

#ifndef _LTISysCh_H

#define _LTISysCh_H

#include "ltisys.h"

class LTISystemChain {

public: // public for demonstration purposes

LTISystem *section; // array of sections

int nsection; // # sections

public:

// constructors

LTISystemChain(int n=1);

LTISystemChain(const LTISystemChain& lch);

~LTISystemChain();

// assignment

LTISystemChain& operator= (const LTISystemChain& lch);

LTISystem& operator[] (int idx);

// clear system

void clear();

// run system

double operator() (double ival);

// frequency response

Complex response(double freq) const;

};

#endif

// butter.cpp -- Butterworth filter design

#include "tools.h"

#include "ltisys.h"

#include "ltisysch.h"

#include "butter.h"

// ButterworthPoles() calculate positions of z-plane

// poles to Butterworth formula

// ButterworthLowPass() build low-pass recursive filter

// to Butterworth design

// ButterworthHighPass() build high-pass recursive filter

// ButterworthBandPass() build band-pass recursive filter

// position nsection poles for Butterworth Low-pass

ComplexWaveform ButterworthPoles(

double freq, // cut-off frequency (fraction)

int nsection // number of 2nd order sections reqd

) // returns array of pole positions

// on positive imaginary axis only

{

// get array of complex values

ComplexWaveform poles(nsection,1);

// calculate angles

double w = PI * freq;

double tanw = sin(w)/cos(w);

// calculate +im pole position for each section

for (int m=nsection;m<=2*nsection;m++) {

// Butterworth formula adapted to z-plane

double ang = (2*m + 1) * PI / (4*nsection);

double d = 1 - 2*tanw*cos(ang) + tanw*tanw;

poles[m-nsection+1] =

Complex((1 - tanw*tanw)/d, 2 * tanw * sin(ang)/d);

}

return poles;

}

// build Butterworth low-pass filter

LTISystemChain ButterworthLowPass(

double freq, // cut-off frequency (fraction)

int nsection // number of 2nd order sections reqd

) // returns array of LTI systems

{

// create empty system chain

LTISystemChain lpfilt(nsection);

// get pole positions

ComplexWaveform pol = ButterworthPoles(freq,nsection);

// convert each conjugate pole pair to

// difference equation

for (int i=0;i<nsection;i++) {

lpfilt[i] = LTISystem(2,2);

// put in conjugate pole pair

lpfilt[i].b[1] = -2.0 * pol[i+1].real();

lpfilt[i].b[2] = pol[i+1].real() * pol[i+1].real() +

pol[i+1].imag() * pol[i+1].imag();

// put 2 zeros at (-1,0)

double tot = 4.0/(1 + lpfilt[i].b[1] + lpfilt[i].b[2]);

lpfilt[i].a[0] = 1.0/tot;

lpfilt[i].a[1] = 2.0/tot;

lpfilt[i].a[2] = 1.0/tot;

}

return lpfilt;

}

// build Butterworth high-pass filter

LTISystemChain ButterworthHighPass(

double freq, // cut-off frequency (fraction)

int nsection // number of 2nd order sections reqd

) // returns array of LTI systems }

{

// create empty system chain

LTISystemChain hpfilt(nsection);

// get pole positions for low-pass

ComplexWaveform pol = ButterworthPoles(0.5-freq,nsection);

// flip all the poles over to get high pass

for (int i=1;i<=nsection;i++)

pol[i] = Complex(-pol[i].real(),pol[i].imag());

// convert each conjugate pole pair to

// difference equation

for (int i=0;i<nsection;i++) {

hpfilt[i] = LTISystem(2,2);

// put in conjugate pole pair

hpfilt[i].b[1] = -2.0 * pol[i+1].real();

hpfilt[i].b[2] = pol[i+1].real() * pol[i+1].real() +

pol[i+1].imag() * pol[i+1].imag();

// put 2 zeros at (1,0)

hpfilt[i].a[0] = 1.0;

hpfilt[i].a[1] = -2.0;

hpfilt[i].a[2] = 1.0;

// normalise to unity gain

double gain = mag(hpfilt[i].response(0.5));

hpfilt[i].a[0] = hpfilt[i].a[0]/gain;

hpfilt[i].a[1] = hpfilt[i].a[1]/gain;

hpfilt[i].a[2] = hpfilt[i].a[2]/gain;

}

return hpfilt;

}

// build Butterworth band-pass filter

LTISystemChain ButterworthBandPass(

double lofreq, // low cut-off frequency (fraction)

double hifreq, // high cut-off frequency (fraction)

int nsection // number of 2nd order sections reqd

) // returns array of LTI systems

{

// force even # sections

if ((nsection%2)==1) nsection++;

// create empty system chain

LTISystemChain bpfilt(nsection);

// get pole positions for low-pass of equivalent width

ComplexWaveform pol = ButterworthPoles(hifreq-lofreq,nsection/2);

// translate the poles to band-pass position

ComplexWaveform bpol(nsection,1);

double wlo = 2*PI*lofreq;

double whi = 2*PI*hifreq;

double ang = cos((whi+wlo)/2)/cos((whi-wlo)/2);

for (int i=1;i<=nsection/2;i++) {

Complex p1 = Complex(pol[i].real()+1,pol[i].imag());

Complex tmp = sqrt(p1*p1*ang*ang*0.25-pol[i]);

bpol[2*i-1] = (p1*ang*0.5) + tmp;

bpol[2*i] = (p1*ang*0.5) - tmp;

}

// convert each conjugate pole pair to

// difference equation

for (int i=0;i<nsection;i++) {

bpfilt[i] = LTISystem(2,2);

// put in conjugate pole pair

bpfilt[i].b[1] = -2.0 * pol[i+1].real();

bpfilt[i].b[2] = pol[i+1].real() * pol[i+1].real() +

pol[i+1].imag() * pol[i+1].imag();

// put zeros at (1,0) and (-1,0)

bpfilt[i].a[0] = 1.0;

bpfilt[i].a[1] = 0.0;

bpfilt[i].a[2] = -1.0;

// normalise to unity gain

double gain = mag(bpfilt[i].response((hifreq+lofreq)/2));

bpfilt[i].a[0] = bpfilt[i].a[0]/gain;

bpfilt[i].a[1] = bpfilt[i].a[1]/gain;

bpfilt[i].a[2] = bpfilt[i].a[2]/gain;

}

return bpfilt;

}

Bibliography

Lynn & Fuerst, Introductory Digital Signal Processing, Chapter 5.

Orfanidis, Introduction to Signal Processing, Chapters 10 & 11.

Example Programs

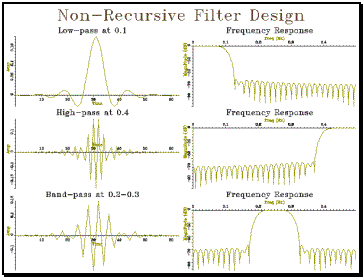
Example 7.1 Non-recursive filter design

// nonrec_t.spc -- test program for non-recursive filter design

#include "tools.h"

#include "ltisys.h"

#include "nonrec.h"

int main()

{

Graph gr(3,2,"Non-Recursive Filter Design");

// calculate low-pass filter and plot

LTISystem lp = NRLowPass(0.1,63);

lp.a.plot(gr,1,"Low-pass at 0.1","Samples","Amp");

// calculate frequency response and plot

Spectrum lpf(500,1000);

for (int i=0;i<500;i++) lpf[i] = lp.response(i/1000.0);

lpf.plotLogMag(gr,2,"Frequency Response");

// calculate high-pass filter and plot

LTISystem hp = NRHighPass(0.4,63);

hp.a.plot(gr,3,"High-pass at 0.4","Samples","Amp");

// calculate frequency response and plot

Spectrum hpf(500,1000);

for (int i=0;i<500;i++)

hpf[i] = hp.response(i/1000.0);

hpf.plotLogMag(gr,4,"Frequency Response");

// calculate band-pass filter and plot

LTISystem bp = NRBandPass(0.2,0.3,63);

bp.a.plot(gr,5,"Band-pass at 0.2-0.3","Samples","Amp");

// calculate frequency response and plot

Spectrum bpf(500,1000);

for (int i=0;i<500;i++) bpf[i] = bp.response(i/1000.0);

bpf.plotLogMag(gr,6,"Frequency Response");

gr.close();

}

Example 7.2 - Demonstrate Kaiser Window

// kaiser_t.cpp -- test program for Kaiser window design

#include "tools.h"

#include "ltisys.h"

#include "nonrec.h"

#include "kaiser.h"

const int MAXKAISERWIN=256; // maximum window length

// Create non-recursive low-pass filter using Kaiser window

LTISystem KaiserLowPass(

double freq, // corner freq

// (fraction of sampling rate)

double ripple, // allowed ripple (dB)

double twidth // transition width

// (fraction of sampling rate) }

) // returns LTI System

{

int i;

// get (half-)Kaiser window

Waveform kwin = Kaiser(ripple,twidth,MAXKAISERWIN);

int nhalf = kwin.count()-1;

// generate one half of coefficients from

// windowed sinc() function

double omega = 2*PI*freq;

for (i=0;i<=nhalf;i++)

kwin[i+1] *= omega*sinc(i*omega)/PI;

// copy into LTI System

LTISystem lpfilt(2*nhalf,0);

lpfilt.a[nhalf] = kwin[1];

for (i=1;i<=nhalf;i++) {

lpfilt.a[nhalf-i] = kwin[i+1];

lpfilt.a[nhalf+i] = kwin[i+1];

}

return lpfilt;

}

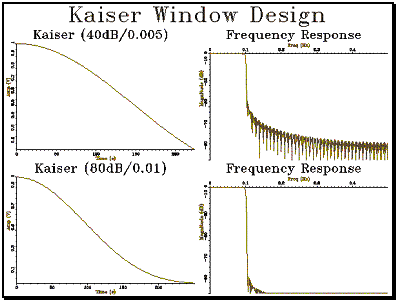
int main()

{

int i;

// initialise graphics

Graph gr (2,2,"Kaiser Window Design");

// plot Kaiser window 1

Waveform kwv1 = Kaiser(40.0,0.005,MAXKAISERWIN);

kwv1.plot(gr,1,"Kaiser (40dB/0.005)");

// calculate and plot frequency response

LTISystem lp1 = KaiserLowPass(0.1,40.0,0.005);

Spectrum lpf1(500,1000);

for (i=0;i<500;i++) lpf1[i] = lp1.response(i/1000.0);

lpf1.plotLogMag(gr,2,"Frequency Response");

// plot Kaiser window 2

Waveform kwv2 = Kaiser(80.0,0.01,MAXKAISERWIN);

kwv2.plot(gr,3,"Kaiser (80dB/0.01)");

// calculate and plot frequency response

LTISystem lp2 = KaiserLowPass(0.1,80.0,0.01);

Spectrum lpf2(500,1000);

for (i=0;i<500;i++) lpf2[i] = lp2.response(i/1000.0);

lpf2.plotLogMag(gr,4,"Frequency Response");

gr.close();

}

Example 7.3 Recursive filter design

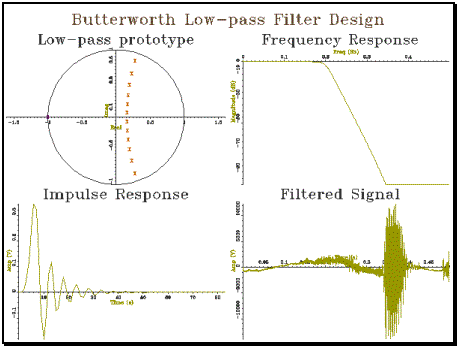
// butter_t.cpp - test program for butterworth filter design

#include "tools.h"

#include "butter.h"

#include "zplane.h"

const double ILIMIT=1.0E-5; // length limit for impulse response

const char *FILENAME="/app/sfs/demo/demo.sfs";

const char *SPITEM="sp.";

const double SAMPLE=0.5;

int main()

{

double fc;

int ns;

cout << "Enter cut-off freq (fraction of sampling rate) : ";

cin >> fc;

cout << "Enter # second order sections : ";

cin >> ns;

// initialise graphics

Graph gr(2,2,"Butterworth Low-pass Filter Design");

// get poles and plot them

ComplexWaveform pol = ButterworthPoles(fc,ns);

ComplexWaveform poles = pol + pol;

for (int i=pol.count()+1;i<=poles.count();i++)

poles[i] = Complex(poles[i].real(),-poles[i].imag());

ComplexWaveform zeros(1,1);

zeros[1] = Complex(-1,0);

PlotZPlane(poles,zeros,gr,1,"Low-pass prototype");

// build chain of second order sections

LTISystemChain lpfilt = ButterworthLowPass(fc,ns);

// calculate frequency response

Spectrum lpfr(500,1000);

for (int i=0;i<500;i++)

lpfr[i] = lpfilt.response(i/1000.0);

lpfr.plotLogMag(gr,2,"Frequency Response");

// measure and plot impulse response

Waveform lpir(0,1);

double lval = 0; // last output

double oval = lpfilt(1.0); // put in unit pulse

while ((fabs(oval) > ILIMIT) || (fabs(oval-lval) > ILIMIT)) {

lpir += oval; // append sample

lval = oval; // remember sample

oval = lpfilt(0.0); // get next sample

}

lpir.plot(gr,3,"Impulse Response");

// plot some filtered speech

Signal isig(1,1.0);

isig.load(FILENAME,SPITEM,0.0,SAMPLE);

Waveform fwv(isig.count(),isig.rate());

lpfilt.clear();

for (int i=1;i<=isig.count();i++)

fwv[i] = lpfilt(isig[i-1]);

fwv.plot(gr,4,"Filtered Signal");

gr.close();

}

Exercises

7.1. Implement a band-pass filter that emulates the telephone system, using a non-recursive filter with 32 coefficients with a response extending from 300Hz to 3500Hz. Use it to filter and display the speech signal /app/sfs/demo/speech.sfs along with some representative spectra and a frequency response curve.

7.2. Adapt the program from exercise 7.1 to use a recursive filter with 2 second-order sections. Find methods for timing the execution speed of programs and compare the efficiency of this program to the original (you may need to comment out the display part for timing).